समकोण त्रिभुज किसे कहते हैं इसके प्रकार, सूत्र और उदाहरण

इस पेज पर आप गणित विषय का महत्वपूर्ण अध्याय समकोण त्रिभुज की समस्त जानकारी पढ़ेंगे।

समकोण त्रिभुज की परिभाषा

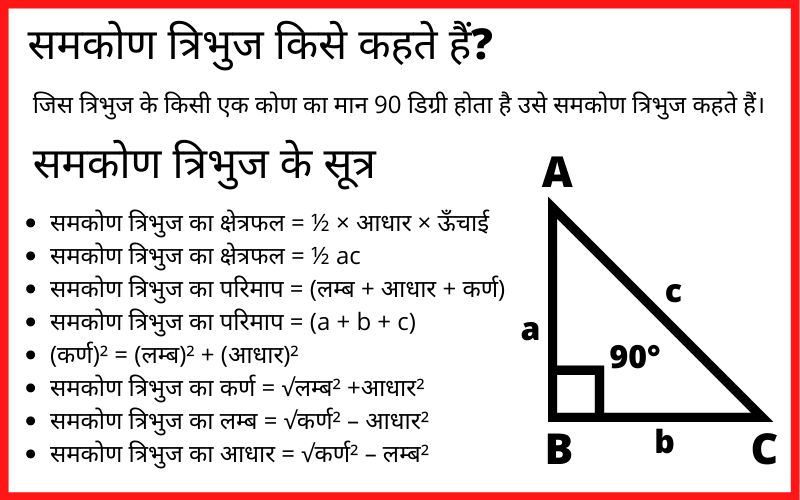
जिस त्रिभुज के किसी एक कोण का मान 90 डिग्री होता है उसे समकोण त्रिभुज कहते हैं।

दूसरे शब्दों में – समकोण त्रिभुज वह त्रिभुज होता है जिसमें 3 भुजाएँ होती हैं और एक कोण समकोण अर्थात 90° का होता हैं। समकोण त्रिभुज की भुजाओं को आधार, कर्ण और ऊँचाई के द्वारा प्रदर्शित किया जाता हैं।

कर्ण :- 90° की भुजा को समकोण त्रिभुज कहाँ जाता हैं।

लम्ब :- जो भुजा आधार के साथ 90 डिग्री का कोण बनाती हैं, उसे लम्ब कहाँ जाता हैं।

आधार :- समकोण त्रिभुज में शेष भुजा को आधार कहाँ जाता हैं।

समकोण त्रिभुज के सूत्र

• समकोण त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
• समकोण त्रिभुज का क्षेत्रफल = ½ ac
• समकोण त्रिभुज का परिमाप ⇒ (लम्ब + आधार + कर्ण) = (a + b + c)
• (कर्ण)² = (लम्ब)² + (आधार)²
• समकोण त्रिभुज का कर्ण = √लम्ब² +आधार²
• समकोण त्रिभुज का लम्ब = √कर्ण² – आधार²
• समकोण त्रिभुज का आधार = √कर्ण² – लम्ब²

समकोण त्रिभुज के प्रकार

गणितज्ञों ने समकोण त्रिभुज को प्रयोग के आधार पर दो भागों में बांटा हैं।

• समद्विबाहु समकोण त्रिभुज
• विषमबाहु समकोण त्रिभुज

1. समद्विबाहु समकोण त्रिभुज

ऐसा समकोण त्रिभुज जिसमें दो भुजाएँ एवं दो कोण आपस में समान हो उस त्रिभुज को समद्विबाहु समकोण त्रिभुज कहलाता हैं।

समद्विबाहु समकोण त्रिभुज में दो कोण 45-45 डिग्री के होते है तथा एक कोण 90 डिग्री का होता हैं। समद्विबाहु समकोण त्रिभुज के सभी कोणों का माप 180 डिग्री होता हैं।

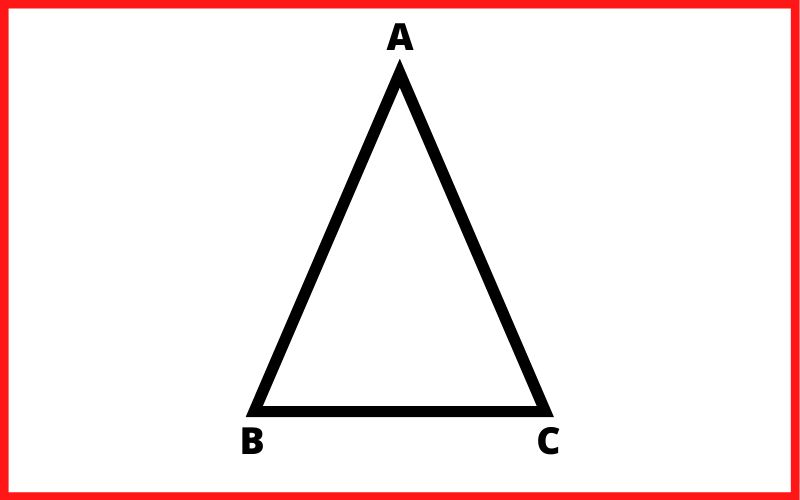
जैसे:-

∠B = 45°
∠A = 90°
∠C = 45°
∠A + ∠B + ∠C = 180°

2. विषमबाहु समकोण त्रिभुज

ऐसा समकोण त्रिभुज जिसकी भुजाओं की लम्बाई अलग-अलग होती हैं तथा कोणों की माप भी अलग-अलग होते हैं। उसे त्रिभुज को विषमबाहु समकोण त्रिभुज कहते हैं।

विषमबाहु समकोण त्रिभुज में एक कोण की माप 30° एवं दूसरे कोण की माप 60° होती हैं। तथा तीसरा कोण 90° का होता हैं।

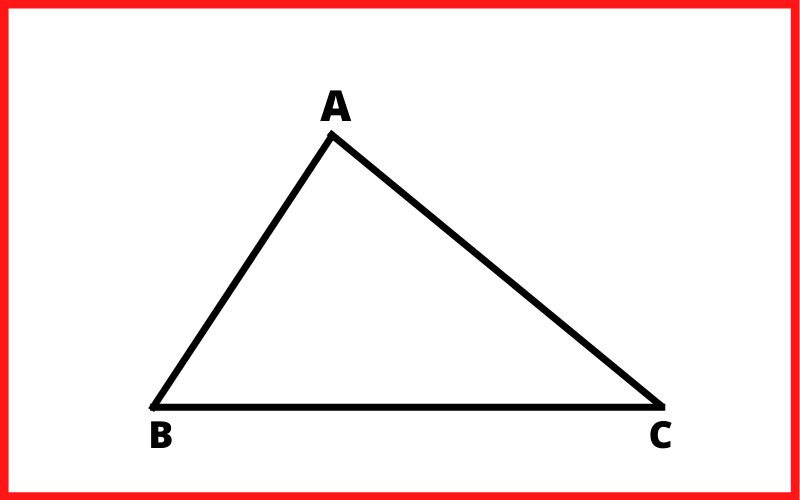
जैसे:-

∠B = 30°
∠A = 90°
∠C = 60°
∠A + ∠B + ∠C = 180°

समकोण त्रिभुज के गुण

• समकोण त्रिभुज में एक कोण हमेशा समकोण होता हैं।
• समकोण त्रिभुज में कर्ण की भुजा सबसे बड़ी भुजा होती हैं।
• अन्य दो आन्तरिक कोणों का योगफल 90 डिग्री होता हैं।
• आधार से लगी दो भुजाएं लम्ब और कर्ण कहलाती हैं।

समकोण त्रिभुज से सम्बंधित प्रश्न-उत्तर

प्रश्न1. एक समकोण त्रिभुज में लम्ब की भुजा 12 सेंटीमीटर हैं आधार की भुजा 9 सेंटीमीटर हैं तो पाइथागोरस के कर्ण की भुजा क्या होगीं?
A. 12 सेंटीमीटर
B. 15 सेंटीमीटर
C. 17 सेंटीमीटर
D. 19 सेंटीमीटर

हल:- प्रश्नानुसार,
पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
AC² = (12)² + (9)²
AC² = 144 + 81
AC² = 225
AC = √225
AC = 15
अतः कर्ण की भुजा 15 होगी।
उत्तर:- 15 सेंटीमीटर

प्रश्न2. एक समकोण त्रिभुज में लम्ब की भुजा 5 सेंटीमीटर हैं आधार की भुजा 12 सेंटीमीटर हैं तो समकोण के कर्ण की भुजा क्या होगीं?
A. 3 सेंटीमीटर
B. 10 सेंटीमीटर
C. 13 सेंटीमीटर
D. 16 सेंटीमीटर

हल:- प्रश्नानुसार,
त्रिभुज समकोण त्रिभुज है, इसलिए पाइथागोरस प्रमेय,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
AC² = (5)² + (12)²
AC² = 25 + 144
AC² = 169
AC = √169
AC = 13
अतः AC की लंबाई 13 सेंटीमीटर होगी।
उत्तर:- 13 सेंटीमीटर

प्रश्न3. त्रिभुज ABC का कोण B समकोण है। यदि AC = 50 सेंटीमीटर और BC = 40 सेंटीमीटर है, तो AB की लम्बाई ज्ञात कीजिए?
A. 30 सेंटीमीटर
B. 60 सेंटीमीटर
C. 90 सेंटीमीटर
D. 120 सेंटीमीटर

हल:- प्रश्नानुसार,
पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
AB² = AC² – BC²
AB² = (50)² – (40)²
AB² = 2500 – 1600
AB² = 900
AB = √900
AB = 30
अतः AB की लम्बाई 30 सेंटीमीटर होगी।
उत्तर:- 30

प्रश्न4. एक समकोण त्रिभुज जिसका आधार 6 सेंटीमीटर तथा कर्ण 10 सेंटीमीटर हैं तो क्षेत्रफल हैं?
A. 24 सेंटीमीटर²
B. 30 सेंटीमीटर²
C. 40 सेंटीमीटर²
D. 48 सेंटीमीटर²

हल:- प्रश्ननानुसार,
आधार = 6 सेंटीमीटर
कर्ण = 10 सेंटीमीटर
पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
AB² = AC² – BC²
AB² = 10² – 6²
AB² = 100 – 36
AB² = 64
AB = √64
AB = 8
उत्तर:- 8 सेंटीमीटर

प्रश्न5. त्रिभुज ABC का कोण B समकोण है। यदि AC = 34 सेमी और AB = 30 सेमी है, तो BC की लम्बाई ज्ञात कीजिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 9 सेंटीमीटर
D. 32 सेंटीमीटर

हल:- प्रश्नानुसार,
AC = 34
AB = 30
BC = ?
त्रिभुज समकोण त्रिभुज है, इसलिए पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
BC² = AC² – AB²
BC² = (34)² – (30)²
BC² = 1156 – 900
BC² = 256
BC = √256
BC = 16
अतः BC की लम्बाई 16 सेंटीमीटर होगी।
उत्तर:- 16 सेंटीमीटर

प्रश्न6. किसी समकोण त्रिभुज का परिमाप उसकी सबसे छोटी भुजा का 6 गुना हैं। भुजाओं का अनुपात क्या होगा?
A. 5 : 3 : 1
B. 7 : 6 : 1
C. 11 : 10 : 4
D. 13 : 12 : 5

हल:- प्रश्ननानुसार,
माना सबसे छोटी भुजा की लम्बाई = x
तथा दूसरी भुजा की लम्बाई = y
समकोण त्रिभुज का कर्ण = √लम्ब² +आधार²
कर्ण = √(x² + y²)
6x = x + y + √(x² + y²)
6x – x – y = √(x² + y²)
5x – y = √(x² + y²)
दोनों पक्षों का वर्ग करने पर
(√x² + y²)² = (5x – y)²
x² + y² = (5x – y)²
x² + y² = 25x² + y² – 2 × 5x × y
x² + y² = 25x² + y² – 10xy
10xy = 25x² – x² + y² – y²
10xy = 24x²
10y = 24x
12x = 5y
x : y = 5 : 12
x : √(x² + y²)
x : √(5² + 12²)
5 : √25 + 144
5 : √169
5 : 13
अभीष्ट अनुपात = 5 : 12 : 13
उत्तर:- 13 : 12 : 5

प्रश्न7. परस्पर समकोण पर काटती हुई 2 मीटर चौड़ी दो सड़के एक आयताकार पार्क जिसका माप 72 मीटर × 48 मीटर के बीच से गुजरती हैं और प्रत्येक सड़क आयत की एक भुजा के समांतर हैं। पार्क के शेष भाग का क्षेत्रफल हैं?
A. 236 वर्ग मीटर
B. 240 वर्ग मीटर
C. 3216 वर्ग मीटर
D. 3220 वर्ग मीटर

हल:- प्रश्ननानुसार,
सड़कों का क्षेत्रफल = L1 + B1 – L2B2
सड़कों का क्षेत्रफल = 72 × 2 + 48 × 2 – 2 × 2
सड़कों का क्षेत्रफल =144 + 96 – 4
सड़कों का क्षेत्रफल = 240 – 4
सड़कों का क्षेत्रफल = 236 वर्ग मीटर
पार्क का क्षेत्रफल = लम्बाई × चौड़ाई
पार्क का क्षेत्रफल = 72 × 48
पार्क का क्षेत्रफल = 3,456
पार्क के शेष भाग का क्षेत्रफल = 3,456 – 236
पार्क के शेष भाग का क्षेत्रफल = 3220 वर्ग मीटर
उत्तर:- 3220 वर्ग मीटर

उम्मीद हैं आपको समकोण त्रिभुज की जानकारी पसंद आयी होगीं। यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ जरूर शेयर करें।