पाइथागोरस प्रमेय क्या हैं इससे संबंधित प्रश्न और उत्तर

इस पेज पर आप पाइथागोरस प्रेमय पढ़िए क्योंकि पाइथागोरस प्रमेय का उपयोग गणित के प्रश्नों को हल करते समय किया जाता हैं।

पिछले पेज पर मैंने क्षेत्रमिति की पोस्ट शेयर की हैं आप वो पोस्ट पढ़कर समस्त जानकारी समझ सकते हैं।

चलिए इस पेज पर पाइथागोरस प्रेमय को पढ़ते और समझते हैं।

पाइथागोरस प्रमेय क्या हैं

यदि कोई भी त्रिभुज पाइथागोरस प्रमेय का पालन करता है, तो वह निश्चित रूप से एक समकोण त्रिभुज है।

पाइथागोरस प्रमेय एक त्रिभुज की भुजाओं के बीच संबंध स्थापित करता हैं। पाइथागोरस प्रमेय की उतपत्ति पाइथागोरस द्वारा की गई थी।

पाइथागोरस ईसा पूर्व छठी शताब्दी के एक यूनानी दार्शनिक थे जिन्होंने समकोण त्रिभुजों का एक आवश्यक गुण घोषित किया था। इसलिए पाइथागोरस के नाम पर ही “पाइथागोरस प्रमेय” का नाम रखा गया।

पाइथागोरस प्रमेय सिद्ध करें

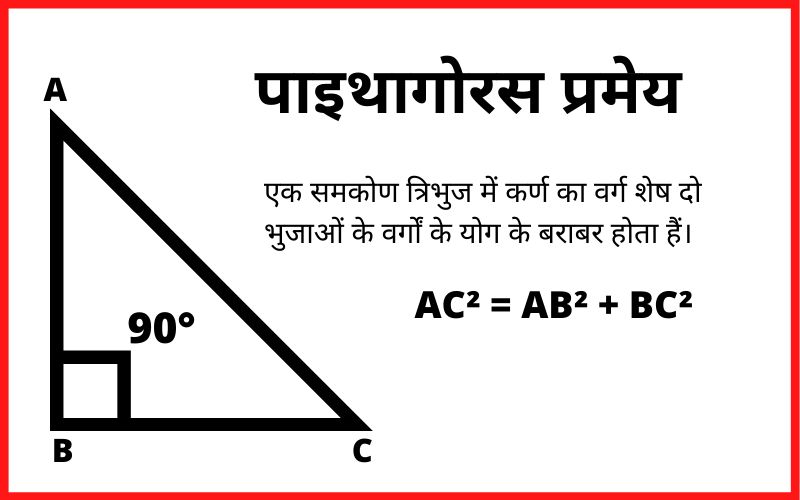
कथन :- एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता हैं।

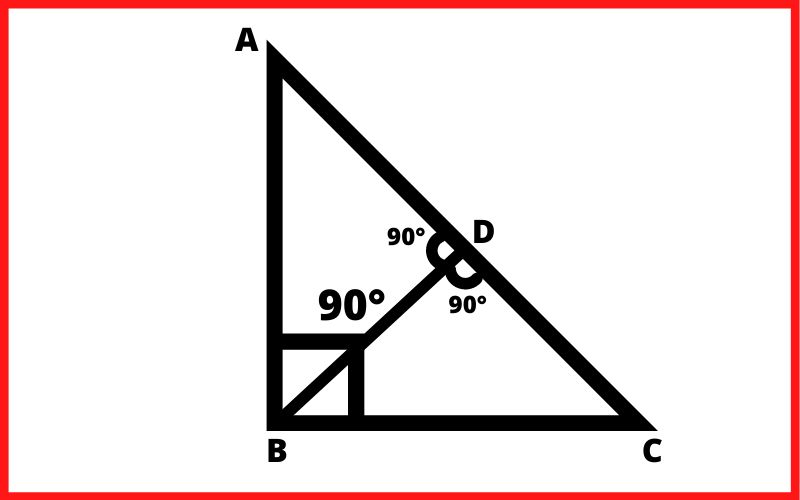
दिया हैं :- ∆ABC में ∠B = 90°

रचना :- BD ⊥ AC

सिद्ध करना हैं :- AC² = AB² + BC²

उत्पत्ति :-
∆ADB व ∆ABC में
∠ADB = ∠ABC = 90°
∠A = ∠A (उभयनिष्ठ)
∆ADB ~ ∆ABC
अतः AD/AB = AB/AC
AD × AC = AB² ………..(1)

∆BDC व ∆ABC में
∠BDC = ∠ABC = 90°
∠C = ∠C (उभयनिष्ठ)
∆BDC ~ ∆ABC
अतः DC/BC = BC/AC
DC × AC = BC² ………..(2)

समीकरण (1) व समीकरण (2) को जोड़ने पर,
AD × AC + DC × AC = AB² + BC²
AC(AD + DC) = AB²+ BC²
AD + DC = AC
AC × AC = AB² + BC²
AC² = AB² + BC²
यहीं सिद्ध करना था।

पाइथागोरस प्रमेय से संबंधित प्रश्न उत्तर

प्रश्न1. एक समकोण त्रिभुज में लम्ब की भुजा 3 सेंटीमीटर हैं आधार की भुजा 4 सेंटीमीटर हैं तो पाइथागोरस के कर्ण की भुजा क्या होगीं?
A. 2 सेंटीमीटर
B. 5 सेंटीमीटर
C. 7 सेंटीमीटर
D. 9 सेंटीमीटर

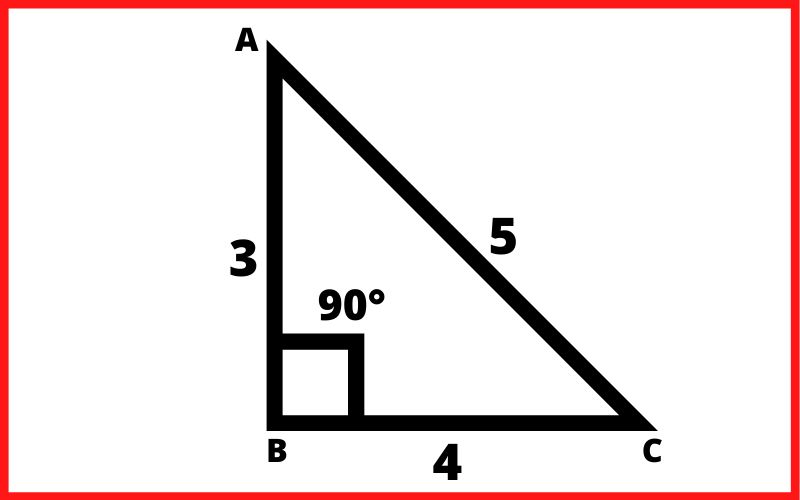
हल:- प्रश्नानुसार,
पाइथागोरस प्रमेय से,
(कर्ण)² = (लम्ब)² + (आधार)²
AC² = AB² + BC²
AC² = (3)² + (4)²
AC² = 9 + 16
AC² = 25
AC = √25
AC = 5
अतः कर्ण की भुजा 5 होगी।
उत्तर:- 5 सेंटीमीटर

प्रश्न2. त्रिभुज ABC का कोण B समकोण है। यदि AB = 5 सेंटीमीटर और BC = 12 सेंटीमीटर है, तो AC की लम्बाई ज्ञात कीजिए?
A. 3 सेंटीमीटर
B. 10 सेंटीमीटर
C. 13 सेंटीमीटर
D. 16 सेंटीमीटर

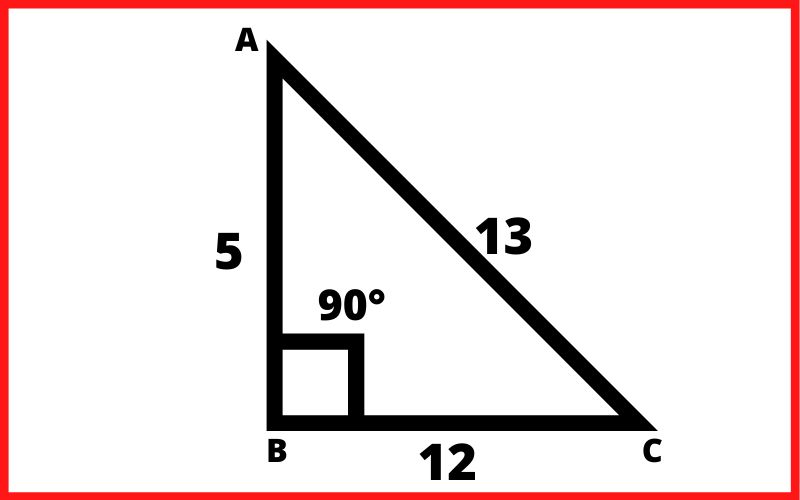
हल:- प्रश्नानुसार,
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
AC² = (5)² + (12)²
AC² = 25 + 144
AC² = 169
AC = √169
AC = 13
अतः AC की लंबाई 13 सेंटीमीटर होगी।
उत्तर:- 13 सेंटीमीटर

प्रश्न3. एक सीढ़ी को एक दीवार से इस प्रकार लगाकर रखी जाती है कि उसका आधार दीवार से 4 मीटर की दूरी पर रहता है और उसका शीर्ष जमीन से 5 मीटर की ऊंचाई पर स्थित एक खिड़की पर लगा होता है। सीढ़ी की लंबाई ज्ञात कीजिए।
A. 1 मीटर
B. 2 मीटर
C. 3 मीटर
D. 4 मीटर

माना AB एक सीढ़ी है और BC दिवार है जिसमें खिड़की C है।
BC = 4 मी. और AC = 5 मी.
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
AB² = AC² – BC²
AB² = (5)² – (4)²
AB² = 25 – 16
AB² = 9
AB = √9
AB = 3
इस प्रकार, सीढ़ी की लंबाई 3 मीटर है।
उत्तर:- 3 मीटर

प्रश्न4. त्रिभुज ABC का कोण B समकोण है। यदि AC = 15 सेंटीमीटर और BC = 12 सेंटीमीटर है, तो AB की लम्बाई ज्ञात कीजिए?
A. 3 सेंटीमीटर
B. 6 सेंटीमीटर
C. 9 सेंटीमीटर
D. 12 सेंटीमीटर

हल:- प्रश्नानुसार,
त्रिभुज समकोण त्रिभुज है, इसलिए पाइथागोरस प्रमेय,
AC² = AB² + BC²
AB² = AC² – BC²
AB² = (15)² – (12)²
AB² = 225 – 144
AB² = 81
AB = √81
AB = 9
अतः AB की लम्बाई 9 सेंटीमीटर होगी।
उत्तर:- 9 सेंटीमीटर

प्रश्न5. त्रिभुज ABC का कोण B समकोण है। यदि AC = 34 सेंटीमीटर और AB = 30 सेंटीमीटर है, तो BC की लम्बाई ज्ञात कीजिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 9 सेंटीमीटर
D. 32 सेंटीमीटर

हल:- प्रश्नानुसार,
AC = 34
AB = 30
BC = ?
त्रिभुज समकोण त्रिभुज है, इसलिए पाइथागोरस प्रमेय,
AC² = AB² + BC²
BC² = AC² – AB²
BC² = (34)² – (30)²
BC² = 1156 – 900
BC² = 256
BC = √256
BC = 16
अतः BC की लंबाई 16 सेंटीमीटर होगी।
उत्तर:- 16 सेंटीमीटर

उम्मीद हैं आपको पाइथागोरस प्रमेय की जानकारी पसंद आयीं होगीं

पाइथागोरस प्रमेय से संबंधित किसी भी प्रश्न के लिए कमेंट करें