इस पेज पर आप गणित के महत्वपूर्ण अध्याय क्षेत्रमिति की जानकारी विस्तार से पढ़ेगे।
पिछली पोस्ट में हम गणित के अध्याय त्रिकोणमिति की जानकारी शेयर कर चुके है उसे जरूर पढ़े।
क्षेत्रमिति थोड़ा सा बड़ा अध्याय है इसलिए आपको समझने और सूत्र याद करने में समय लगेगा। लेकिन दो-तीन बार इस पोस्ट को पड़कर आप क्षेत्रमिति को समझकर इसके सभी प्रश्न आसानी से हल कर पाएंगे।
क्षेत्रमिति किसे कहते है
क्षेत्रमिति के अंतर्गत हम द्विविमीय और त्रिविमीय आकृति के बारे में पड़ते है। जहाँ हम आयतन, क्षेत्रफल, परिमाप या परिमिति आदि को निकालना सीखते है।
द्विविमीय आकृतियां :- आयत, वर्ग, समकोण त्रिभुज, समद्विबाहु त्रिभुज, समबाहु त्रिभुज, विषमबाहु त्रिभुज आदि।
त्रिविमीय आकृतियां :- घन, घनाभ, बेलन, शंकु, गोला, शंकु का छिन्नक आदि।
क्षेत्रमिति में हम आयतन, क्षेत्रफल, आदि को निकालना सीखते है।
क्षेत्रफल (AREA) : किसी आकृति का उसके सभी भुजाओं से घिरे हुए तल को उस आकृति का क्षेत्रफल कहते हैं क्षेत्रफल की इकाई (Unit) वर्गमीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
परिमाप/परिमिति (PERIMETER) : किसी आकृति का सभी भुजाओं की लंबाइयों का योग उस आकृति का परिमाप या परिमिति कहलाता हैं परिमाप की इकाई (unit) मीटर, सेंटीमीटर, किलोमीटर आदि होती हैं।
त्रिभुज (TRIANGLE)
तीन भुजाओं से घिरा समतल क्षेत्र त्रिभुज कहलाता हैं त्रिभुज के लिए ‘∆’ चिन्ह का प्रयोग किया जाता हैं किसी भी त्रिभुज में तीन भुजाएं, तीन शीर्ष तथा तीन कोण होते हैं त्रिभुज के तीनों कोणों का योग 180° होता हैं।
1. समबाहु त्रिभुज (Equilateral Triangle) : जिस त्रिभुज की तीनों भुजाएं बराबर हों उसे समबाहु त्रिभुज कहते हैं समबाहु त्रिभुज के प्रत्येक कोण का मान 60° होता हैं।
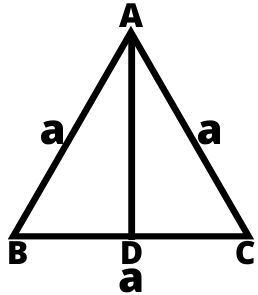
- समबाहु त्रिभुज का क्षेत्रफल = √3/4 × भुजा²
- समबाहु त्रिभुज का परिमाप = 3 × भुजा
- शीर्ष बिंदु से डाले गए लम्ब की लम्बाई = √3/4 × भुजा
2. समद्विबाहु त्रिभुज (Isosceles Triangle) : जिस त्रिभुज की किन्हीं दो भुजाओं की लम्बाई बराबर हों, उसे समद्विबाहु त्रिभुज कहते हैं।
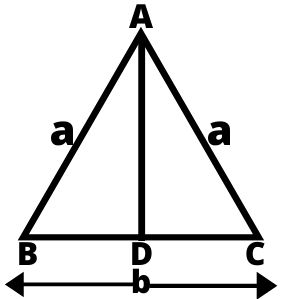
- समद्विबाहु त्रिभुज का क्षेत्रफल = b¼(4a² – b²)
- समद्विबाहु त्रिभुज का परिमाप = a + a + c या 2a + b
- शीर्ष बिंदु A से डाले गए लम्ब की लम्बाई AD = ½(√4a² – b²)
3. विषमबाहु त्रिभुज (Scalene Triangle) : जिस त्रिभुज की तीनों भुजाएं असमान लम्बाई की हो, उसे विषमबाहु त्रिभुज कहते हैं।
उदाहरण: AB बराबर नहीं होता BC के, BC बराबर नहीं होता CA के।
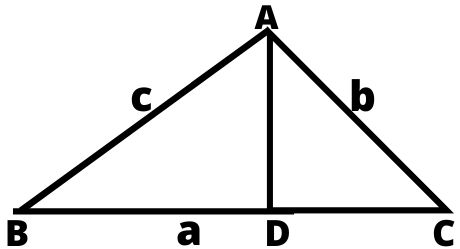
- विषमबाहु त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
- विषमबाहु त्रिभुज का परिमाप = तीनों भुजाओं का योग = (a + b + c)/2
- विषमबाहु त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
4. समकोण त्रिभुज (Right-Angle Triangle) : जिस त्रिभुज का एक कोण समकोण अर्थात 90° का हो, उसे समकोण त्रिभुज कहते हैं।
यदि समकोण त्रिभुज में ∠ABC के समकोण होने के साथ-साथ AB और BC की लम्बाईया भी बराबर हों, तो त्रिभुज ABC को समद्विबाहु समकोण त्रिभुज ABC को समद्विबाहु समकोण त्रिभुज कहते है।
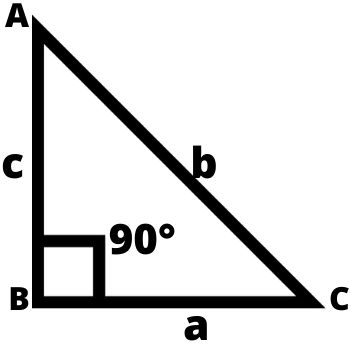
- समकोण त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
- समकोण त्रिभुज का क्षेत्रफल = ½ ac
- समकोण त्रिभुज का परिमाप = (लम्ब + आधार + कर्ण) = (a + b + c)
- समकोण त्रिभुज का कर्ण = √लम्ब² +आधार²
- समकोण त्रिभुज का लम्ब = √कर्ण² – आधार²
- समकोण त्रिभुज का आधार = √कर्ण² – लम्ब²
5. न्यूनकोण त्रिभुज (Acute Angled Triangle) : जिस त्रिभुज के तीनों कोण न्यून कोण अर्थात 90° से कम हो, उसे न्यूनकोण त्रिभुज कहते हैं।
त्रिभुज ABC में प्रत्येक कोण की माप 90° से कम हैं।
6. अधिक कोण त्रिभुज (Obtuse-angled triangle) : जिस त्रिभुज का एक कोण अधिक कोण अर्थात 90° से अधिक हो, उसे अधिक कोण त्रिभुज कहते हैं त्रिभुज ABC में ∠ABC की माप 90° से अधिक हैं।
चतुर्भुज (QUADRILATERAL)
चार भुजाओं से घिरे समतल क्षेत्र को चतुर्भुज कहते हैं किसी भी चतुर्भुज में चार भुजाएँ तथा चार कोण होते हैं चतुर्भुज के चारों कोणों का योगदान चार समकोण अर्थात 360° का होता हैं।
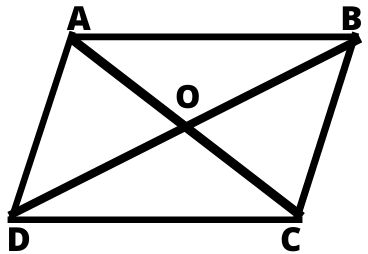
रेखाखण्ड AC तथा BD को विकर्ण कहते हैं चतुर्भुज की वे दो भुजाएँ, जिसका कोई उभयनिष्ठ बिंदु न हो, सम्मुख भुजाएँ कहलाती हैं, AB, CD तथा AD, BC सम्मुख भुजाएँ हैं।
1. समान्तर चतुर्भुज (Parallelogram) : चार भुजाओं से घिरी वह आकृति, जिसके आमने-सामने की भुजाएँ बराबर और समान्तर हों, समान्तर चतुर्भुज कहलाती हैं इसमें सम्मुख कोण भी बराबर होते हैं।
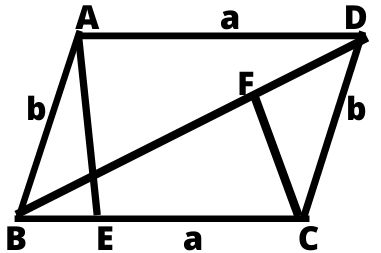
ABCD एक समान्तर चतुर्भुज हैं जिसमें भुजा AB, CD के और AD, BC के समांतर तथा बराबर हैं BD समान्तर चतुर्भुज का विकर्ण तथा AE इसकी ऊँचाई हैं।
यदि समान्तर चतुर्भुज ABCD की भुजाएँ a, b हो और A से BC पर डाले गए लम्ब AE की लम्बाई h हो, तो
- समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई = ah
- समान्तर चतुर्भुज का क्षेत्रफल = कर्ण × आमने सामने के शीर्ष से कर्ण की लम्बाई दूरी = BD × CF
- समान्तर चतुर्भुज का क्षेत्रफल = 2 × त्रिभुज ABD या BCD का क्षेत्रफल
- समान्तर चतुर्भुज का परिमाप = भुजाओं का योगदान = 2 × (a × b)
2. आयत (Rectangle) : चार भुजाओं से घिरी वह आकृति, जिसमें आमने सामने की भुजाएँ समान्तर और बराबर होती हैं तथा प्रत्येक कोण समकोण होता हैं, उसे आयत कहते हैं।
AC तथा BD को विकर्ण कहते हैं तथा ये आपस में बराबर होते हैं अर्थात AC = BD
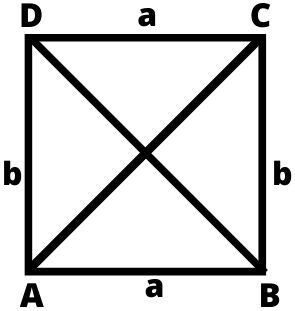
- आयत का परिमाप = 2(लम्बाई + चौड़ाई)
- आयत का क्षेत्रफल = लंबाई ×चौड़ाई
- आयत का विकर्ण =√(लंबाई² + चौड़ाई²)
आयात से सम्बन्धित कुछ महत्वपूर्ण सिध्दांत
- जब किसी आयत में एक विकर्ण डाला जाए तो उसमें बने दो त्रिभुज के क्षेत्रफल समान होगें।
- जब आयत में दो विकर्ण डाले जाए तो दोनों की लम्बाई समान होगी और आमने सामने के कोण भी समान होगें।
- जब किसी आयत के अंदर बड़े से बड़े वृत्त को बनाया जाए तब आयत की चौड़ाई वृत्त के व्यास के बराबर होती हैं। तो अन्तः वृत्त का क्षेत्रफल (πb²/ 4) होता हैं।
- जब आयत के बाहर की तरफ वृत्त बना हो तब आयत का विकर्ण वृत्त के व्यास के बराबर होता हैं।
Case#1:
आयत की चौड़ाई = वृत का व्यास
चौड़ाई / 2 = वृत्त की त्रिज्या
b/2 = r
r = b/2
दोनों पक्षों का वर्ग करने पर
πr² = π(b/2)²
आयत के अन्तः वृत्त का क्षेत्रफल = (πb²)/4
Case#2:
आयत के विकर्ण = वृत्त का व्यास
विकर्ण/2 = वृत्त की त्रिज्या
r = D/2
दोनों पक्षों का वर्ग करने पर
π r² = π (D/2)²
आयत के बाह्य वृत का क्षेत्रफल = (πD²)/4
Case#3:
आंतरिक वृत और बह्यवृत के अनुपातों का क्षेत्रफल
आंतरिक वृत : बह्यवृत
त्रिज्या का अनुपात = b : d
परिधि का अनुपात = b : d
क्षेत्रफल का अनुपात = b² : d²
Note:
- जब किसी आयत के अंतवृत और बाह्यवृत्त के संबंधों का अनुपात दर्शाया जाए।
- त्रिज्या और परिधि के अनुपात हमेशा समान होगें, इनके वर्ग करने पर क्षेत्रफल का अनुपात प्राप्त हो।
- आयत की चौथाई और विकर्ण ही अंतवृत और बह्यवृत की त्रिज्या और परिधि के अनुपात होते हैं।
3. विषमकोण समचतुर्भुज (Rhombus) : चार भुजाओं से घिरी वह आकृति, जिसमें चारों भुजाएं बराबर हों, लेकिन एक भी कोण समकोण न हो, उसे विषमकोण समचतुर्भुज या समचतुर्भुज कहते हैं।
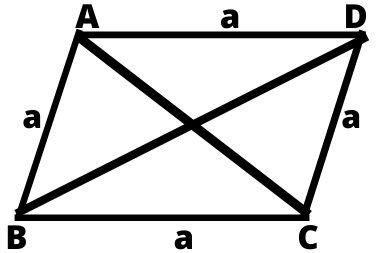
- विषमकोण चतुर्भुज का क्षेत्रफल = ½ × दोनों विकर्णो का गुणनफल
- विषम कोण समचतुर्भुज की परिमाप = 4 × एक भुजा
- समचतुर्भुज में (AC)² + (BD)² = 4a²
समचतुर्भुज के विकर्ण एक दूसरे को 90° पर दो बराबर भागों में विभाजित करते हैं।
4. वर्ग (square) : चार भुजाओं से घिरी वह आकृति जिसकी चारो भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण अर्थात 90° का हो, उसे वर्ग कहते हैं।
AC तथा BD को विकर्ण कहते हैं तथा ये आपस में एक दूसरे के बराबर होते हैं अर्थात AC = BD
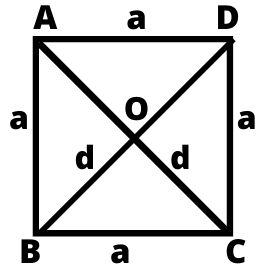
- वर्ग का क्षेत्रफल = (एक भुजा)² = a²
- वर्ग का क्षेत्रफल = ½ × (विकर्णो का गुणनफल) = ½ × AC × BD
- वर्ग की परिमिति = 4 × a
- वर्ग का विकर्ण = एक भुजा × √2 = a × √2
- वर्ग का विकर्ण = √2 × वर्ग का क्षेत्रफल
Case#1: जब वर्ग के अंदर बड़ा से बड़ा वृत्त बना हो।
अन्तः वृत्त का क्षेत्रफल = (π a²)/4
Case#2. जब वर्ग के बाहर बड़े से बड़ा वृत्त बना हो।
बाह्य वृत्त का क्षेत्रफल:- (πa²)/2
Note:-
- आंतरिक वृत और बह्यवृत के वर्ग में हमेशा 1 : √2 होता हैं।
- परिधि का अनुपात = 1 : √2
- क्षेत्रफल का अनुपात = 1 : 2
- वर्ग के क्षेत्रफल का अनुपात = 1 : 2
Case#3:- जब वर्ग के विकर्ण पर वर्ग बनाया जाए
भुजाओं का अनुपात = 1 : √2
क्षेत्रफलों का अनुपात = 1 : 2
Case#4:- जब वर्ग के विकर्ण पर समबाहु त्रिभुज बनाया जाए
भुजाओं का अनुपात = 1 : √2
क्षेत्रफलों का अनुपात = 2 : √3
5. समलम्ब चतुर्भुज (Trapezium) : चार भुजाओं से घिरी वह आकृति, जिसकी केवल दो भुजाएँ समान्तर हों, उसे समलम्ब चतुर्भुज कहते हैं।
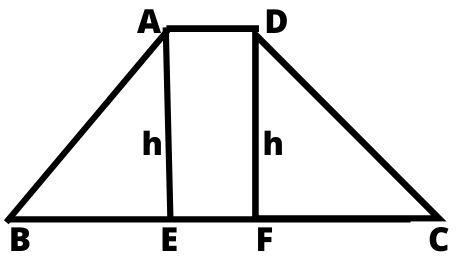
ABCD एक समलम्ब चतुर्भुज हैं, जिसमें सिर्फ AD तथा BC समान्तर भुजाएँ हैं AB और CD आड़ी (oblique) भुजाएँ हैं A से AE या D से DF लम्ब BC पर खींचा जाए तो AE या DF इसकी ऊँचाई होगी।
- समलम्ब चतुर्भुज का क्षेत्रफल = ½ × ऊँचाई × समान्तर भुजाओं का योग
- समलम्ब चतुर्भुज का क्षेत्रफल = ½ × h × (AD + BC)
बहुभुज (POLYGON)
बहुभुज का क्षेत्रफल उसको कई त्रिभुजों या चतुर्भुजों या अन्य मानक आकृतियों में बांटकर निकाला जाता हैं यदि बहुभुज में पाँच, छः या दस भुजाएँ हों, तो उसको क्रमशः पंचभुज, छट्भुज, दसभुज कहाँ जाता हैं।
- n भुजा वाले चतुर्भुज का अन्तः कोणों का योग = 2(n -2) × 90°
- n भुजा वाले बहुभुज के बहिष्कोणों का योग = 360°
- n भुजा वाले समबहुभुज का प्रत्येक अन्तः कोण = [2(n – 2) × 90°] / n
- n भुजा वाले समबहुभुज का प्रत्येक भहिष्यकोण = 360°/n
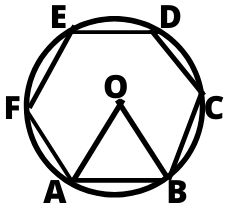
- बहुभुज की परिमिति = n × एक भुजा
- नियमित षट्भुज का क्षेत्रफल = 6 × ¼√3 (भुजा)²
- नियमित षट्भुज का क्षेत्रफल = 3√3×½ (भुजा)²
- नियमित षट्भुज की परिमति = 6 × भुजा
- समषट्भुज की भुजा = परिवृत की त्रिज्या
- n भुजा वाले नियमित बहुभुज के विकर्णो की संख्या = n(n – 3)/2
वृत्त (CIRCLE)
वृत्त एक ऐसी बिंदु का बिंदुपथ हैं, जो इस तरह घूमता हैं कि उसकी दूरी एक स्थिर बिंदु से सदैव बराबर रहती हैं स्थिर बिंदु को वृत्त का केंद्र, अचल दूरी को वृत्त की त्रिज्या एवं अर्द्व्यास तथा बिंदु पथ को परिधि कहते हैं।
केंद्र से गुजरने वाली वह सीधी रेखा जो वृत्त को दो बराबर खंडों में विभक्त करती हैं वृत्त का व्यास कहलाती हैं, वृत्त का व्यास उसकी त्रिज्या का दोगुना होता हैं।
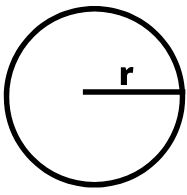
किसी वृत्त की परिधि की लंबाई उसकी व्यास की लंबाई की लगभग 22/7 गुना होती हैं इसे ग्रीक अक्षर π द्वारा प्रदर्शित किया जाता हैं अक्षर π को पाई पड़ा जाता हैं, जहाँ π = परिधि/व्यास = 22/7 = 3.1428571 होता हैं।
परिधि पर स्थित किन्हीं दो बिंदुओं को मिलाने वाली सीधी रेखा को वृत्त की जीवा या चाप कर्ण कहते हैं।
- वृत्त का व्यास = 2 × त्रिज्या = 2r
- वृत्त की परिधि = 2π त्रिज्या = 2πr
- वृत्त की परिधि = π × व्यास = πd
- वृत्त का क्षेत्रफल = π × त्रिज्या² = πr²
- वृत्त की त्रिज्या = √वृत्त का क्षेत्रफल/π
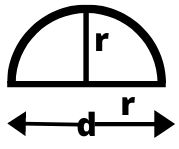
- अर्द्ववृत्त की परिमिति = (n + 2)r = (π + 2)d/2
- अर्द्ववृत्त का क्षेत्रफल = 1/2πr² = 1/8 πd²
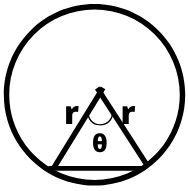
- त्रिज्याखण्ड का क्षेत्रफल = θ/360° × वृत्त क्षेत्रफल = θ/360° × πr²
- त्रिज्याखण्ड की परिमिति = (2 + πθ/180°)r
- वृतखण्ड का क्षेत्रफल = (πθ/360° – 1/2 sinθ)r²
- वृतखण्ड की परिमिति = (L + πrθ)/180° , जहाँ L = जीवा की लम्बाई
- चाप की लम्बाई = θ/360° × वृत्त की परिधि
- चाप की लम्बाई = θ/360° × 2πr
- दो संकेन्द्रीय वृत्तों जिनकी त्रिज्याए R1, R2, (R1 ≥ R2) हो तो इन वृत्तों के बीच का क्षेत्रफल = π(r²1 – r²2)
आयतन (VOLUME) : कोई वस्तु जितना स्थान घेरती हैं, उसे उस वस्तु का आयतन कहते हैं आयतन की इकाई (unit) घन मीटर, घन सेंटीमीटर, घन किलोमीटर आदि होती हैं।
सतह (SURFACE) : जिस पृष्ठों द्वारा वस्तु घिरी होती हैं उसे उस वस्तु की सतह कहते हैं सतह, पृष्ठों का क्षेत्रफल होता हैं, इस कारण इसकी इकाई (unit) वर्ग मीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
घनाभ (CUBOID)
छः पृष्ठों से घिरी वह आकृति, जिसमें प्रत्येक पृष्ठ एक आयत होता हैं और सम्मुख पृष्ठ बराबर होते हैं घनाभ कहलाती हैं।
घनाभ एक ऐसी त्रिआयामी (3d) आकृति है जिसके 6 आयताकार फलक होते हैं। इसी वजह से ऐसी आकृतियों को बहुफलक भी कहा जाता है।
जैसे:- किताब, ईट, दियासलाई की डिबिया संदूक इत्यादि।
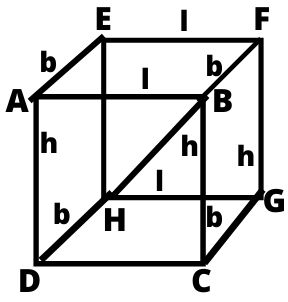
- घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
- घनाभ का आयतन = l × b × h
- घनाभ का परिमाप = 2(l + b) × h
- घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
- घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
- घनाभ के विकर्ण = √(लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
- घनाभ का विकर्ण = √l² + b² + h²
आयताकार कमरा (RECTANGULAR ROOM) :
- कमरे की चारों दीवारों का क्षेत्रफल = 2 × ऊँचाई × (लम्बाई + चौड़ाई)
- छत या फर्श का क्षेत्रफल = लम्बाई × चौड़ाई
- कमरे का विकर्ण = √ (लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
- खोखले बेलन का आयतन = πh(r^21 – r^22)
- खोखले बेलन का वक्र पृष्ठ = 2πh(r^21 + r^22)
- खोखले बेलन का सम्पूर्ण पृष्ठ = 2πh(r1 + r2) + 2π(r^21 – r^22)
घन (Cube)
घन एक ऐसी त्रिआयामी आकृति को कहा जाता है जिसकी लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं।
एक घन में छः फलक, बारह किनारे एवं आठ कोने होते हैं इसके छह बराबर-बराबर आकार के फलक होते हैं हर फलक एक वर्ग होता हैं और छह फलक होने के कारण यह एक प्रकार का षट्फलकी (hexahedron) भी कहलाता हैं।
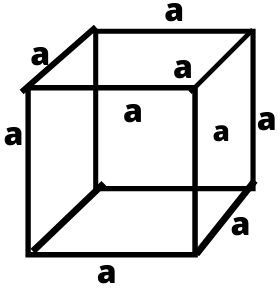
- घन का आयतन = a × a × a
- घन का परिमाप = 4 × a × a
- घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6 a² वर्ग सेंटीमीटर।
- घन का विकर्ण = √3a सेंटीमीटर।
बेलन (Cylinder)
बेलन ज्यामिति में एक त्रिआयामी ठोस की आकृति है। इसका पार्श्व पृष्ठ वक्र, सिरे समान त्रिज्या के वृत्ताकार होते हैं, बेलन सरल रूप में एक रोलर या समान व्यास का गिलास है।
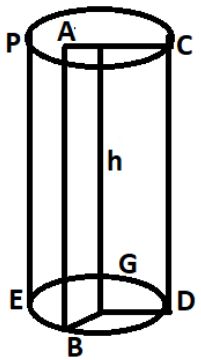
- बेलन का आयतन = πr²h
- बेलन के वक्र पृष्ठ का क्षेत्रफल = 2πrh
- बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल = (2πrh + 2πr²h) वर्ग सेंटीमीटर।
शंकु (Cone)
शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
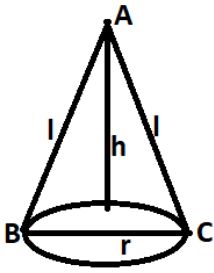
- L = √(r² + h²)
- शंकु का आयतन = (πr²h)/3 घन सेंटीमीटर।
- शंकु का वक्र पृष्ठ का क्षेत्रफल = πrl वर्ग सेंटीमीटर।
- शंकु का सम्पूर्ण पृष्ठ का क्षेत्रफल = (πrl + πr²) वर्ग सेंटीमीटर।
गोला (Sphere)
गोला वह ठोस है जिसमें केवल एक तल होता है और इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता है। इस बिन्दु को गोले का केन्द्र कहते हैं तथा केन्द्र से गोले के किसी बिन्दु की दूरी को गोले की त्रिज्या कहते हैं।
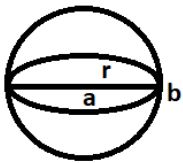
- गोला का आयतन = (4πr³)/3 घन सेंटीमीटर
- गोले का वक्र पृष्ठ = 4πr² वर्ग सेंटीमीटर
- अर्द्धगोले का आयतन = (2πr³)/3 घन सेंटीमीटर
- अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr² वर्ग सेंटीमीटर
- अर्द्वगोले की त्रिज्या r हो, तो
- अर्द्वगोले का आयतन = 2/3 πr³
- अर्द्वगोले का वर्कप्रष्ठ = 2πr²
- अर्द्वगोले का सम्पूर्ण पृष्ठ = 3πr²
शंकु का छिन्नक (Frustum of a Cone)
शंकु के कुछ उपरी भाग को आधार के समान्तर समतल द्वारा काट देने पर बचे ठोस को शंकु का छिन्नक कहते है।
- शंकु के छिन्नक का आयतन = (πh)/3 (R² + r² + Rr)
- तिर्यक भाग का क्षेत्रफल = π (R + r)³, l² = h² + (R – r)²
- छिन्नक के सम्पूर्ण पृष्ठ का क्षेत्रफल = π[R² + r² + l(R + r)]
द्विविमीय आकृतियों के सूत्र
- त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
- समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
- वृत्त का क्षेत्रफल = πr² (जहाँ r वृत्त की त्रिज्या हैं।)
- वृत्त की परिधि = 2πr
- वृत्त की त्रिज्या = परिधि/2r
- समबाहु त्रिभुज का क्षेत्रफल = (√3/4) × भुजा × भुजा
- समबाहु त्रिभुज का परिमाप = 3 × भुजा
- शीर्ष बिंदु से डाले गए लम्ब की लम्बाई = (√3/4) × भुजा
- समद्विबाहु त्रिभुज का क्षेत्रफल = (a × √4b²- a²)/4
- समद्विबाहु त्रिभुज का परिमाप = a + 2b
- शीर्ष बिंदु A से डाले गए लम्ब की लम्बाई = (√4b² – a²)/2
- विषमबाहु त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
- विषमबाहु त्रिभुज का परिमाप = तीनों भुजाओं का योग = (a + b + c)/2
- विषमबाहु त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
- आयत का परिमाप = 2(l + b)
- आयत का क्षेत्रफल = l × b
- आयत का विकर्ण =√(l² + b²)
- वर्ग का परिमाप = 4a
- वर्ग का क्षेत्रफल = भुजा × भुजा
- वर्ग का विकर्ण = √2a
- कमरे की चार दीवारों का क्षेत्रफल = 2 × (लम्बाई + चौड़ाई) × ऊँचाई
क्षेत्रमिति के उदाहरण
Q1. एक त्रिभुज के तीनों कोणों का योग कितना होता हैं?
A. 90°
B. 180°
C. 270°
D. 360°
Ans. 180°
Q2. एक त्रिभुज की भुजाएं क्रमशः 3 सेंटीमीटर, 4 सेंटीमीटर, और 5 सेंटीमीटर हैं इसका क्षेत्रफल क्या होगा?
A. 6
B. 8
C. 10
D. 12
हल:- प्रश्ननानुसार,
a = 3 सेंटीमीटर
b = 4 सेंटीमीटर
c = 5 सेंटीमीटर
त्रिभुज की तीनों भुजाओं का योग = (a + b + c)/2
s = (3 + 4 + 5)/2
s = 12/2
s = 6
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ = √6(6 – 3)(6 – 4)(6 – 5)
∆ = √6 × 3 × 2 × 1
∆ = √36
∆ = 6
Ans. 6 वर्ग सेंटीमीटर।
Q3. एक त्रिभुज के आधार की लम्बाई 15 मीटर तथा ऊँचाई 12 मीटर हैं, एक दूसरे त्रिभुज का क्षेत्रफल इस त्रिभुज के क्षेत्रफल का दुगुना हैं तथा इस त्रिभुज के आधार की लंबाई 20 मीटर हैं, इस त्रिभुज की ऊँचाई क्या होंगी?
A. 18 मीटर
B. 8 मीटर
C. 28 मीटर
D. 38 मीटर
हल:- पहले त्रिभुज का क्षेत्रफल = ½ × आधार × ऊँचाई
= ½ (15 × 12)
= 90 वर्ग मीटर
दूसरे त्रिभुज का क्षेत्रफल = 2 × 90
क्षेत्रफल = 180 वर्ग मीटर
आधार = 20 मीटर
दूसरे त्रिभुज की ऊंचाई = (क्षेत्रफल × 2)/आधार
= (180 × 2)/20
Ans. 18 मीटर।
Q.4 एक समकोण त्रिभुज जिसका आधार 6 सेमी. तथा कर्ण 10 सेमी. हैं, तो क्षेत्रफल हैं?
A. 24 सेमी.²
B. 30 सेमी.²
C. 40 सेमी.²
D. 48 सेमी.²
हल:- समकोण ∆ की ऊँचाई = √(10² – 6²)
= √(100 – 36)
= √64
= 8 सेमी.
∆ का क्षेत्रफल = ½ × आधार × ऊँचाई
∆ का क्षेत्रफल = ½ × 6 × 8
∆ का क्षेत्रफल = 24 सेमी.²
Ans. 24 सेमी.²
Q.5 एक त्रिभुज की भुजाएँ क्रमशः 3 सेमी. 4 सेमी. और 5 सेमी. हैं त्रिभुज का क्षेत्रफल हैं?
A. 6 वर्ग सेमी.
B. √23 वर्ग सेमी.
C. √12 वर्ग सेमी.
D. √32 सेमी.
हल:- प्रश्ननानुसार,
त्रिभुज की भुजाएँ क्रमशः 3 सेमी. 4 सेमी. और 5 सेमी. हैं।
a = 3, b = 4, c = 5
S = (a + b + c)/2
S = (3 + 4 + 5)/2
S = 12/2
S = 6 सेंटीमीटर
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ का क्षेत्रफल = √6(6 – 3)(6 – 4)(6 – 5)
∆ का क्षेत्रफल = √6 × 3 × 2 × 1
∆ का क्षेत्रफल = √6 × 6
∆ का क्षेत्रफल = 6 वर्ग सेमी.
Ans. 6 वर्ग सेमी.
Q.6 किसी त्रिभुज का परिमाप 30 सेमी. और उसका क्षेत्रफल 30 वर्ग सेमी. हैं यदि त्रिभुज की सबसे बड़ी भुजा की लम्बाई 13 सेमी. हैं, तो उसकी सबसे छोटी भुजा की लम्बाई क्या हैं?
A. 3 सेमी.
B. 4 सेमी.
C. 5 सेमी.
D. 6 सेमी.
हल:- माना,
कि त्रिभुज की सबसे छोटी भुजा = x सेमी.
तब, मध्य की भुजा = 30 – (13 + x)
= 30 – 13 – x
= (17 – x) सेमी.
प्रश्ननानुसार,
a = 13, b = x, c = 17 – x
S = (a + b + c)/2
S = (13 + x + 17 – x)/2
S = 30/2
S = 15 सेंटीमीटर
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
30 = √15(15 – 13)(15 – x)(15 – 17 – x)
30 = √15 × 2 × (15 – x)(2 – x)
(30)² = 30 × (15 – x)(x – 2)
900 = 30 × (15x – 30 – x² + 2x)
900/30 = (17x² – x² – 30)
x² + 17x – 30 – 30 = 0
x² + 17x – 60 = 0
x² – 17x + 60 = 0
x² – 12x – 5x + 60 = 0
x(x – 12) – 5(x – 12) = 0
(x – 12)(x – 5) = 0
x – 12 = 0, x – 5 = 0
x = 12, x = 5
सबसे छोटी भुजा = 5 सेमी.
Ans. 5 सेमी.
Q.7 किसी त्रिभुज की भुजाएँ 3 सेमी. 4 सेमी. और 5 सेमी. हैं इस त्रिभुज की भुजाओं के मध्य बिन्दुओ को मिलाने से बने त्रिभुज का क्षेत्रफल (सेमी.³ में) हैं?
A. 6 वर्ग सेमी.
B. 3 वर्ग सेमी.
C. 1.5 वर्ग सेमी.
D. 3.4 वर्ग सेमी.
हल:- मध्य बिंदुओ को मिलाने वाली रेखा सामने की भुजा की आधी होती हैं तब भुजाएँ क्रमशः 1.5 सेमी. 2 सेमी. तथा 2.5 सेमी. होगी तथा बना त्रिभुज समकोण होगा।
अभीष्ट क्षेत्रफल = ½ × आधार × लम्ब
= ½ × 1.5 × 2
= 1.5 वर्ग सेमी.
Ans. 1.5 वर्ग सेमी.
Q.8 एक त्रिभुज की भुजाएँ 5 : 4 : 3 के अनुपात में हैं यदि त्रिभुज की परिमाप 24 सेमी. हैं, तो त्रिभुज का क्षेत्रफल क्या होगा?
A. 12 वर्ग सेमी.
B. 24 वर्ग सेमी.
C. 6 वर्ग सेमी.
D. 48 वर्ग सेमी.
हल:- माना त्रिभुज की भुजाएँ = 5x, 4x और 3x
प्रश्ननानुसार,
5x + 4x + 3x = 24
12x = 24
x = 2
अतः भुजाएँ 10, 8 और 6 सेमी.
a = 10, b = 8, c = 6
S = (a + b + c)/2
S = (10 + 8 + 6)/2
S = 24/2
S = 12 सेमी.
∆ का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ का क्षेत्रफल = √12(12 – 10)(12 – 8)(12 – 6)
∆ का क्षेत्रफल = √12 × 2 × 4 × 6
∆ का क्षेत्रफल = √24 × 24
∆ का क्षेत्रफल = 24 वर्ग सेमी.
Ans. 24 वर्ग सेमी.
Q.9 यदि समबाहु ∆ की एक भुजा 4√3 सेमी. हैं तो उसका क्षेत्रफल होगा?
A. 12/√3 वर्ग सेमी.
B. 24/√3 सेमी.
C. 12/√3 सेमी.
D. 21/√3 सेमी.
हल:- समबाहु ∆ का क्षेत्रफल = √3/4 + (भुजा)²
= √3/4 × (4√3)²
= √3/4 × 16 × 3
= √3 × 4 × 3
= 12√3
Ans. 12√3
Q.10 यदि किसी समबाहु त्रिभुज का क्षेत्रफल √3 सेमी.^2 हो, तो उसकी भुजा (सेमी. में) होगी?
A. 1
B. 2
C. 3
D. 4
हल:- √3/4 × भुजा² = √3 सेंटीमीटर²
भुजा = √4
भुजा = 2 सेंटीमीटर
Ans. 2
Q.11 किसी समबाहु त्रिभुज का क्षेत्रफल 400√3 वर्ग मीटर हैं इसका परिमाप हैं?
A. 120 मीटर
B. 150 मीटर
C. 90 मीटर
D. 135 मीटर
हल:- समबाहु त्रिभुज का क्षेत्रफल = √3/4 × (भुजा)²
400√3 = √3/4 × (भुजा)²
भुजा = 40
त्रिभुज का परिमाप = 40 × 3
= 120 मीटर
Ans. 120 मीटर
Q.12 एक समबाहु त्रिभुज जिसका क्षेत्रफल 4√3 वर्ग सेमी. हैं, कि भुजा हैं?
A. 1 सेमी.
B. 2 सेमी.
C. 3 सेमी.
D. 4 सेमी.
हल:- समबाहु त्रिभुज का क्षेत्रफल = √3/4 (भुजा)²
प्रश्ननानुसार,
√3/4 (भुजा)² = 4√3
भुजा² = 4²
भुजा = 4 सेंटीमीटर.
Ans. 4 सेंटीमीटर
Q.13 किसी त्रिभुज PQR की भुजाएँ 5 सेमी. 12 सेमी. तथा 13 सेमी. हैं त्रिभुज में एक अन्तः वृत्त बनाया गया हैं उस वृत्त का क्षेत्रफल (वर्ग सेमी.) में हैं?
A. 4π
B. 3π/4
C. π
D. 4
हल:- माना,
वृत्त की त्रिज्या r सेमी. हैं
r = √1/15(15 – 5)(15 – 12)(15 – 13)
r = √1/15 × 10 × 3 × 2
r = √4
r = 2 सेमी.
वृत्त का क्षेत्रफल = πr²
= π2²
= 4π
Ans. 4π
Q14. एक आयताकार मैदान की लंबाई और चौड़ाई का अनुपात 7 : 3 हैं यदि मैदान का क्षेत्रफल 189 मीटर^2 हो तो मैदान के चारों और तीन बार लपेटने में कुल कितना तार लपेटना पड़ेगा?
A. 50 मीटर
B. 150 मीटर
C. 180 मीटर
D. 250 मीटर
हल:- आयताकार मैदान की लंबाई = 7x मीटर
तथा आयताकार मैदान की चौड़ाई = 3x मीटर
आयताकार मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
189 = (7x) × (3x)
189 = 21 x²
x² = 189/21
x² = 9
x = 3 मीटर
अतः लम्बाई = 7x
7 × 3 = 21 मीटर
तथा चौड़ाई = 3x
3 × 3 = 9 मीटर
आयताकार मैदान का परिमाप = 2(लम्बाई + चौड़ाई)
= 2(21 + 9)
= 60 मीटर
अतः तीन चक्कर में लपेटा गया कुल तार = 3 × परिमाप
= 3 × 60
Ans. 180 मीटर
Q15. एक आयताकार क्षेत्रफल की लम्बाई और चौड़ाई क्रमशः 40 मीटर और 30 मीटर हैं उस आयताकार क्षेत्रफल का परिमाप क्या होगा?
A. 140
B. 170
C. 200
D. 280
हल:- आयताकार क्षेत्रफल का परिमाप
लम्बाई = 40 मीटर
चौड़ाई = 30 मीटर
आयत का परिमाप = 2(l + b)
= 2(40 + 30)
= 2 × 70
Ans. 140 मीटर
Q16. एक आयत की लम्बाई 15 सेंटीमीटर और इसके विकर्ण की लम्बाई 17 सेंटीमीटर हो तो आयत का क्षेत्रफल कितना होगा?
A. 120 वर्ग सेंटीमीटर
B. 220 वर्ग सेंटीमीटर
C. 60 वर्ग सेंटीमीटर
D. 180 वर्ग सेंटीमीटर
हल:- विकर्ण = 17 सेंटीमीटर
लम्बाई = 15 सेंटीमीटर
आयत का विकर्ण =√(l² + b²)
17 = √l² + (15)²
(17)² = l² + (15)²
(17)² – (15)² = l²
289 – 225 = l²
L² = 64
L = 8
आयत का क्षेत्रफल = l × b
= 8 × 15
Ans. 120 वर्ग सेंटीमीटर।
Q17. एक कमरा 20 मीटर लम्बा हैं और 15 मीटर चौड़ा हैं इसके फर्श पर 60 सेंटीमीटर चौड़ी दरी बिछाने का खर्च 20 रूपए/मीटर की दर से कितना होगा।
A. 10,000
B. 20,000
C. 5,000
D. 15,000
हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 20 × 15
= 300 मीटर।
क्षेत्रफल = लम्बाई × चौड़ाई
300 = l × 60/100
5 = l/100
L = 500
= 500 × 20
= 10,000
Ans. 10,000
Q18. एक आयताकार पार्क की लम्बाई 90 मीटर और चौड़ाई 60 मीटर हैं, इसके अंदर चारों और 5 मीटर चौड़ा रास्ता हैं, इस रास्ते पर 15 रूपए/वर्ग मीटर की दर से रुड़ी बिछाने का खर्च कितने रूपए होगा?
A. 8000 रूपए
B. 11000 रूपए
C. 31000 रूपए
D. 21000 रूपए
हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 90 × 60
= 5400 वर्ग मीटर
क्षेत्रफल = लम्बाई × चौड़ाई
= 80 × 50
= 40,000 वर्ग मीटर
रास्ते का क्षेत्रफल = 5400 – 4000
= 1400 वर्ग मीटर
= 1400 × 15
= 21000 रूपए
Ans. 21000 रूपए।
Q.19 यदि एक समबाहु त्रिभुज की प्रत्येक भुजा उस वृत्त की त्रिज्या के बराबर हैं, जिसका क्षेत्रफल 154 वर्ग सेमी. हैं तो समबाहु त्रिभुज का क्षेत्रफल क्या होगा?
A. 7√3 वर्ग सेमी.
B. 49√3/4 वर्ग सेमी.
C. 35/√4 सेमी.
D. 49 वर्ग सेमी.
हल:- वृत्त का क्षेत्रफल = πr²
154 = 22/7 × r²
r² = (154 × 7) × 22
r² = 7 × 7
r² = 7²
r = 7
त्रिभुज की भुजा = 7 सेंटीमीटर
त्रिभुज का क्षेत्रफल = √3/4 × 49
= 49√3/4 वर्ग सेमी.
Ans. 49√3 / 4 वर्ग सेमी.
Q.20 उस बड़े से बड़े त्रिभुज का क्षेत्रफल जो एक अर्द्व वृत्त, जिसकी त्रिज्या r हैं, के अंतर्गत बनाया जा सकता हैं होगा?
A. 2r² सेमी.
B. r² वर्ग सेमी.
C. 2 r² वर्ग सेमी.
D. r/2 वर्ग सेमी.
हल:- त्रिभुज का क्षेत्रफल = ½ × 2r × r
= r² वर्ग सेमी .
Ans. r² वर्ग सेमी.
Q.21 एक आयताकार भूखण्ड की लम्बाई और चौड़ाई में अनुपात 5 : 3 हैं यदि लम्बाई चौड़ाई से 6 मीटर अधिक हो, तो भूखण्ड का क्षेत्रफल क्या हैं?
A. 135 वर्ग मीटर
B. 280 वर्ग मीटर
C. 300 वर्ग मीटर
D. 800 वर्ग मीटर
हल:- माना,
आयताकार भूखण्ड की लम्बाई 5x मीटर हैं।
तथा चौड़ाई = 3x मीटर
5x – 3x = 6
2x = 6
x = 3
लम्बाई = 5 × 3
लम्बाई = 15 मीटर
तथा चौड़ाई = 3 × 3
चौड़ाई = 9 मीटर
भूखण्ड का क्षेत्रफल = 15 × 9
= 135 वर्ग मीटर
Ans. 135 वर्ग मीटर
Q.22 परस्पर समकोण पर काटती हुई 2 मीटर चौड़ी दो सड़के एक आयताकार पार्क जिसका माप 72 मी. × 48 मी. हैं के बीच से गुजरती हैं और प्रत्येक सड़क आयत की एक भुजा के समांतर हैं पार्क के शेष भाग का क्षेत्रफल हैं?
A. 236 वर्ग मीटर
B. 240 वर्ग मीटर
C. 3216 वर्ग मीटर
D. 3220 वर्ग मीटर
हल:- सड़कों का क्षेत्रफल = 27 × 2 + 48 × 2 – 2 × 2
= 144 + 96 – 4
= 144 + 92
= 236 वर्ग मी.
पार्क के शेष भाग का क्षेत्रफल = 72 × 48 – 236
= 3220 वर्ग मी.
Ans. 3220 वर्ग मी.
Q.23 एक आयताकार खेत का क्षेत्रफल 396 वर्ग मीटर हैं उसकी लम्बाई 22 मीटर हैं, तो चौड़ाई और परिमिति क्या होगी?
A. 80 मीटर
B. 90 मीटर
C. 60 मीटर
D. 50 मीटर
हल:- आयत का क्षेत्रफल = लम्बाई × चौड़ाई
चौड़ाई = 396/22
चौड़ाई = 18 मी.
परिमिति = 2(लम्बाई + चौड़ाई)
= 2(22 + 18)
= 2 × 40
= 80 मीटर
Ans. 80 मीटर
Q24. एक आयताकार खेत के चारों और अंदर से सीमा से लगा हुआ 8 मीटर चौड़ा रास्ता बना हैं यदि खेत को लम्बाई और चौड़ाई क्रमशः 180 मीटर और 150 मीटर हो तो रास्ता का क्षेत्रफल क्या होगा?
A. 2,014 वर्ग मीटर
B. 3,024 वर्ग मीटर
C. 4,879 वर्ग मीटर
D. 5,024 वर्ग मीटर
हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 180 × 150
= 27000 वर्ग मीटर
क्षेत्रफल = लम्बाई × चौड़ाई
= 164 × 134
= 21,976 वर्ग मीटर
रास्ते का क्षेत्रफल = 27000 – 21,976
= 5024
Ans. 5,024 वर्ग मीटर।
Q25. एक आयत का क्षेत्रफल 252 वर्ग सेंटीमीटर हैं, इसकी लम्बाई तथा चौड़ाई 9 : 7 हैं, इसका परिमाप क्या हैं?
A. 87 सेंटीमीटर
B. 56 सेंटीमीटर
C. 87 सेंटीमीटर
D. 64 सेंटीमीटर
हल:- आयत का क्षेत्रफल = 252
लम्बाई = 9
चौड़ाई = 7
9x × 7x = 252
63x^2 = 252
x^2 = 4
x = 2
9 × 2 = 18
7 × 2 = 14
आयत का परिमाप = 2(l + b)
= 2(18 + 14)
= 2 × 32
= 64
Ans. 64 सेंटीमीटर।
क्षेत्रमिति के प्रश्न-उत्तर
Q26. यदि किसी आयताकार भूखण्ड की लम्बाई में 5% की वृद्धि और चौड़ाई में 10% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
A. 2.4%
B. 6.9%
C. 4.9%
D. 5.5%
हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 100% × 100%
= (105% × 90%)/100
= 189/2
= 94.5%
= 100% – 94.5%
= 5.5%
Ans. 5.5% की कमी होगी।
Q27. एक आयत का विकर्ण 10 सेंटीमीटर हैं तथा यह आयत की लम्बाई का 2 गुना हैं, बताइए आयत का क्षेत्रफल कितना हैं?
A. 15√3
B. 25√3
C. 5√3
D. 35√3
हल:- आयत का विकर्ण =√(l² + b²)
10 = √(5)² + b²
10^2 = 5² + b²
100 = 25 + b²
b² = 100 – 25
b² = 75
b = 5√3
क्षेत्रफल = लम्बाई × चौड़ाई
= 5 × 5√3
= 25√3
Ans. 25√3 वर्ग सेंटीमीटर।
Q28. 28 सेंटीमीटर लम्बे और 14 सेंटीमीटर चौड़े आयत के अंतर्गत खींचे जाने वाले वृत्त का क्षेत्रफल कितना हैं?
A. 154
B. 121
C. 169
D. 225
हल:- अन्तः वृत्त का क्षेत्रफल = (πb²/ 4) होता हैं।
= (22 ×7 × 7)/7
= 22 × 7
= 154
Ans. 154 सेंटीमीटर।
Q.29 एक समकोणीय त्रिभुज आकृति के चारागाह जिसकी दो परस्पर लम्ब भुजाओं की लम्बाई क्रमशः 6 व 8 मीटर है के प्रत्येक शीर्ष पर एक-एक घोड़े 3 मीटर की रस्सी से बाधे जाते हैं चारागाह के कितने क्षेत्रफल को वे चर पायेंगे?
A. 9π/2 (मी.)²
B. 10π/3 (मी.)²
C. 17π/4 (मी.)²
D. 31π/2 (मी.)²
हल:- अभीष्ट क्षेत्रफल = 180°/360° × π × 3²
= 1/2 × 9π
= 9π/2 (मी.)²
Ans. 9π/2(मी.)²
Q.30 किसी वर्ग की लम्बाई में बढ़ोतरी 40% तथा चौड़ाई में 40% कमी की जाती हैं परिणामी आयत तथा वर्ग के क्षेत्रफलों में अनुपात होगा?
A. 21 : 25
B. 31 : 35
C. 21 : 40
D. 15 : 16
हल:- यदि वर्ग की प्रत्येक भुजा 100 सेमी. हैं, तो आयत की लंबाई = 140 सेंटीमीटर
तथा आयत की चौड़ाई = 60 सेंटीमीटर
आयत का क्षेत्रफल : वर्ग का क्षेत्रफल
= 8400 : 10000
= 21 : 25
Ans. 21 : 25
Q.31 यदि एक समचतुर्भुज का क्षेत्रफल 15 वर्ग सेमी. तथा उसके एक विकर्ण की लम्बाई 5 सेमी. हो तो, दूसरे विकर्ण की लम्बाई होगी?
A. 3 सेमी.
B. 4 सेमी.
C. 5 सेमी.
D. 6 सेमी.
हल:- समचतुर्भुज का क्षेत्रफल = ½ × एक विकर्ण × दूसरा विकर्ण
15 = ½ × 5 × दूसरा विकर्ण
दूसरा विकर्ण = (15 × 2)/5
= 6 सेमी.
Ans. 6 सेमी.
Q.32 किसी समचतुर्भुज का परिमाप 40 मीटर हैं और उसकी ऊँचाई 5 मीटर हैं इसका क्षेत्रफल हैं?
A. 20 वर्ग मीटर
B. 30 वर्ग मीटर
C. 40 वर्ग मीटर
D. 50 वर्ग मीटर
हल:- समचतुर्भुज की एक भुजा = 40/4
= 10 मीटर
तथा ऊँचाई = 5 मीटर
अभीष्ट क्षेत्रफल = 10 × 5
= 50 वर्ग मीटर
Ans. 50 वर्ग मीटर
Q.33 किसी कमरे की चारों दीवारों का क्षेत्रफल 128 वर्ग मीटर हैं यदि लम्बाई और चौड़ाई आपस मे बराबर हैं तथा ऊँचाई 4 मीटर हैं तो कमरे के फर्श का क्षेत्रफल हैं?
A. 40 वर्ग मीटर
B. 60 वर्ग मीटर
C. 64 वर्ग मीटर
D. 68 वर्ग मीटर
हल:- कमरे के चारों दीवारों का क्षेत्रफल = 2 (लम्बाई + चौड़ाई) × ऊँचाई
माना,
कि लम्बाई = x मीटर
तो चौड़ाई = x मीटर
2 ( x + x) × 4 = 128
16x = 128
x = 128/16
x = 8 मीटर
फर्श का क्षेत्रफल = लम्बाई × चौड़ाई
= 8 × 8
= 64 वर्ग मीटर
Ans. 64 वर्ग मीटर
Q34. उस वर्ग का क्षेत्रफल कितना होगा जिसके विकर्ण की लंबाई 6 सेंटीमीटर हैं?
A. 28 सेंटीमीटर
B. 38 सेंटीमीटर
C. 8 सेंटीमीटर
D. 18 सेंटीमीटर
उत्तर:- क्षेत्रफल = d²/2
= (6 × 6)/2
= 18
Ans. 18 सेंटीमीटर।
Q35. एक वर्ग की प्रत्येक भुजा की लम्बाई में 20% की वृद्धि करने पर उसके क्षेत्रफल में कितने प्रतिशत की वृद्धि होगी?
A. 44% की वृद्धि।
B. 84% की हानि।
C. 44% की वृद्धि।
D. 54% की हानि।
हल:- क्षेत्रफल = भुजा × भुजा
= [(100% + 20%) × (100% + 20%)]/100
= (120 × 120)/100
= 144
= 144 – 100
= 44%
Ans. 44% की वृद्धि।
Q36. किसी वर्गाकार खेत की भुजा 45 मीटर हैं उस खेत का क्षेत्रफल होगा?
A. 1560
B. 3053
C. 3590
D. 2025
हल:- क्षेत्रफल = भुजा × भुजा
= 45 × 45
Ans. 2025
Q37. 120 मीटर भुजा केवर्गाकार मैदान के बीचों बीच परस्पर समकोण पर काटती हुए 20 मीटर चौड़ी दो पट्टियां बनी हैं, बताइए पट्टियों को कर शेष मैदान का क्षेत्रफल कितना होगा?
A. 10,000
B. 20,000
C. 5,000
D. 15,000
हल:- क्षेत्रफल = भुजा × भुजा
= 120 × 120
= 14,400 वर्ग मीटर
क्षेत्रफल = भुजा × भुजा
= (120 × 120) + (120 × 120)
= 2400 + 2400
= 4800
क्षेत्रफल = भुजा × भुजा
= 20 × 20
= 400
= 4800 – 400
= 4400
शेष मैदान का शेषफल = 14,400 – 4400
Ans. 10,000
Q38. एक वर्ग की प्रत्येक भुजा की लम्बाई में 25% की वृद्धि करने पर उसके क्षेत्रफल में कितने प्रतिशत की वृद्धि होगी?
A. 48.98%
B. 46.25% की वृद्धि।
C. 56.25% की वृद्धि।
D. 90.67%
हल:- क्षेत्रफल = भुजा × भुजा
= [(100% + 25%) × (100% + 25%)]/100
= (125 × 125)/100
= 625/4
= 156.25
= 156.25 – 100
= 56.25%
Ans. 56.25% की वृद्धि।
Q39. किसी आयत की लम्बाई और चौड़ाई क्रमशः 35 मीटर और 30 मीटर हैं, इसमें से 5 मीटर भुजा की कितनी वर्गाकार क्यारियां बनाई जा सकती हैं?
A. 42
B. 55
C. 68
D. 90
हल:- (बड़ी वस्तु का क्षेत्रफल)/(छोटी वस्तु का क्षेत्रफल)
= (35 × 30)/(5 × 5)
= 7 × 6
Ans. 42
Q40. एक आयत और एक वर्ग के क्षेत्रफल समान हैं यदि आयत की लम्बाई 90 मीटर और चौड़ाई 80 मीटर हैं तो वर्ग की भुजा ज्ञात कीजिए?
A. 50√2
B. 60√2
C. 40√2
D. 30√2
हल:- आयत का क्षेत्रफल = वर्ग का क्षेत्रफल
लम्बाई × चौड़ाई = a²
90 × 80 = a²
7200 = a²
a² = 7200
a = √7200
a = 60√2
Ans. 60√2
Q41. एक त्रिभुजाकर खेत की भुजाएं क्रमशः 20 मीटर, 21 मीटर तथा 29 मीटर लम्बी हैं इस खेत में 25 रूपए प्रति वर्ग मीटर की दर से फसल काटने का खर्च क्या होगा?
A. 4280 रूपए
B. 3950 रूपए
C. 5250 रूपए .
D. 5900 रूपए
हल:- a = 20, b = 21, c = 29
s = (a + b + c)/2
s = (20 + 21 + 29)/2
s = 70/2
s = 35
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
= √35 (35 – 20) (35 – 21) (35 – 29)
= √35 × 15 × 14 × 6
= √210 × 210
= 210
= 210 × 25 रूपए
Ans. 5250 रूपए
Q42. एक समकोण त्रिभुज का आधार 12 सेंटीमीटर तथा कर्ण 13 सेंटीमीटर हैं इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए?
A. 60 वर्ग सेंटीमीटर
B. 90 वर्ग सेंटीमीटर
C. 30 वर्ग सेंटीमीटर
D. 50 वर्ग सेंटीमीटर
हल:- AC² = AB² + BC²
(13)² = (AB)² + (12)²
169 = (AB)² + 144
169 – 144 = (AB)²
(AB)² = 25
AB = 5
त्रिभुज का क्षेत्रफल = ½ (आधार × ऊँचाई)
= ½ (12 × 5)
= 6 × 5
Ans. 30 वर्ग सेंटीमीटर।
Q43. 280 मीटर के बराबर व्यास के वृत्तीय क्षेत्रफल के चारों ओर एक 7 मीटर चौड़े बगीचे के निर्माण की लागत क्या होगी यदि बगीचे के निर्माण के लिए प्रति वर्ग मीटर लागत 21 रूपए हैं?
Ans. 1,32,594
Q.44 यदि दो वर्गों के क्षेत्रफलों में अनुपात 25 : 36 हैं, तो उनके परिमापों में अनुपात होगा?
A. 1 : 2
B. 2 : 1
C. 4 : 3
D. 5 : 6
हल:- वर्ग की भुजाओं का अनुपात = √25/√36
= 5/6
परिमापों का अनुपात = (5 × 4)/(6 × 4)
= 5 : 6
Ans. 5 : 6
Q.45 6.5 मी. × 4.0 मी. की माप वाले एक कमरे के फर्श का वर्गाकार संगमरमर के टुकड़ों से सुसज्जित करना हैं ऐसे बड़े से बड़े सम्भव टुकड़े की लम्बाई होगी?
A. 20 सेमीमीटर
B. 50 सेमीमीटर
C. 100 सेमीमीटर
D. 180 सेमीमीटर
हल:- कमरे की लंबाई = 650 सेमी. तथा
चौड़ाई = 400 सेमी.
अब, 650 और 400 का महत्तम समापवर्तक = 50
अतः प्रत्येक संगमरमर के टुकड़े का साइज = 50 × 50 सेमीमीटर
अतः बड़े से बड़े सम्भव टुकड़े की लम्बाई = 50 सेमी.
Ans. 50 सेमी.
Q.46 एक अर्द्ध गोलाकार खिड़की जिसका व्यास 63 सेमीमीटर हैं कि परिधि क्या होगी?
A. 111 सेमीमीटर
B. 121 सेमीमीटर
C. 158 सेमीमीटर
D. 162 सेमीमीटर
हल:- r = 63/2
गोलाकार खिड़की की परिधि = 2πr/2 + 2r
= 22/7 × 63/2 + 2 × 63/2
= 99 + 63
= 162 सेमीमीटर
Ans. 162 सेमीमीटर
Q.47 एक पहिए का व्यास 1.26 मी. हैं यह 500 चक्कर में कितनी दूरी तय करेगा?
A. 1679 मीटर
B. 1980 मीटर
C. 2487 मीटर
D. 3870 मीटर
हल:- पहिए की परिधि = 22/7 × 1.26
= 3.96 मीटर
500 चक्करों को पूरा करने में चली गई दूरी = 3.96 × 500
= 1980 मीटर
Ans. 1980 मीटर
Q.48 एक वृताकार मैदान के चारों ओर एक वृताकार सड़क हैं जिसके अंदर के घेरे और बाहर के घेरे की लम्बाईयों का अंतर 88 मी. हैं सड़क की चौड़ाई हैं। (π = 22/7)
A. 68 मीटर
B. 45 मीटर
C. 8 मीटर
D. 14 मीटर
हल:- प्रश्ननानुसार,
2πR – 2πr = 88
2π(R – r) = 88
R – r = 88/2π
R – r = 88 / 2 × 22/7
R – r = (88 × 7) / 2 × 22
R – r = 2 × 7
R – r = 14
सड़क की चौड़ाई = R – r = 14 मीटर
Ans. 14 मीटर
Q.49 वर्ग के रूप में मुड़ा हुआ एक तार का क्षेत्रफल 484 वर्ग सेमीमीटर हैं यदि वही तार एक वृत्त के रूप में तोड़ दिया जाए तो घिरने वाला क्षेत्रफल होगा?
A. 587 सेमीमीटर
B. 616 सेमीमीटर
C. 872 सेमीमीटर
D. 987 सेमीमीटर
हल:- 2πr = 4 × √484
= 4 × 22
= 88 सेमीमीटर
अतः 2πr = 88 सेमीमीटर
r = 88/2 × 7/22
r = 14 सेमीमीटर
वृत्त का क्षेत्रफल = 22/7 × 14 × 14
= 616 सेमीमीटर
Ans. 616 सेमीमीटर
Q.50 यदि किसी वृत्त की त्रिज्या दूनी कर दी जाए, तो नए वृत्त की परिधि तथा व्यास में क्या अनुपात होगा?
A. π/2
B. 2π
C. π
D. π + 2
हल:- माना वृत्त की त्रिज्या = r
वृत्त की परिधि = 2πr
वृत्त की त्रिज्या = 2r
वृत्त की परिधि = 2.2πr
= 4πr
नए वृत्त का व्यास = 2.2r
= 4r
अनुपात = 4πr/4r
अनुपात = π
Ans. π
क्षेत्रमिति से सम्बंधित नीचे कुछ प्रश्न दिए गए हैं जिन्हें आपको ही हल करना हैं और साथ ही प्रश्न के उत्तर भी दिए गए जो सही हैं आप इन प्रश्नों को हल कीजिए और दिए गए उत्तर से मैच कीजिए यदि आपका उत्तर सही आता हैं तो आप इस टॉपिक को अच्छे से समझ गए होंगे और यदि अभी भी आपको कोई डाउट हैं या इन प्रश्नों को करने में यदि आपको कोई प्रॉब्लम हैं या प्रश्न समझ नहीं आ रहा हैं तो मुझे कमेंट द्वारा जरूर बताए आप 15 प्रश्नों में से कितने प्रश्नों को सही से हल कर पाते हैं कमेंट द्वारा जरूर बताएं तो चलिए प्रश्नों को पढ़िए और जल्दी से उनको हल कीजिए।
Q1. 120 मीटर लम्बाई और 80 मीटर चौड़ाई के आयताकार क्षेत्रफल के बीचों बीच अंदर की तरफ 8 मीटर चौड़ा दो परस्पर समकोण पर काटते हुए दो रास्ते बने हैं, उस रास्ते का क्षेत्रफल बताइए?
Ans. 1,536
Q2. किसी कमरे के फर्श की माप 10 मीटर और 8 मीटर हैं इस पर अधिकतम माप की कितनी वर्गाकार डिजाइन बनाई जा सकती हैं?
Ans. 20
Q3. किसी वर्ग के अंतवृत की त्रिज्या 2√7 सेंटीमीटर हैं बताइए वर्ग के परिवृत्त का क्षेत्रफल कितना हैं?
Ans. 176 सेंटीमीटर।
Q4. 25 मीटर लम्बे 20 मीटर चौड़े आयताकार खेत से बनाए गए बड़े से बड़े वर्गाकार क्षेत्र का क्षेत्रफल कितना हैं?उत्तर:- 400
Q5. 8 मीटर लम्बे और 6 मीटर चौड़े कमरे में 16 मीटर चौड़ा कालीन बिछाया गया उस कालीन की लम्बाई कितनी हैं?
Ans. 30 मीटर।
Q6. आयताकार खेत की लम्बाई, चौड़ाई से 20 मीटर अधिक हैं खेत के चारों ओर बाढ़ लगाने का खर्च 26.50 रूपए की दर से 5300 रूपए हैं बताइए उस खेत की लम्बाई कितनी हैं?
Ans. 60 मीटर।
Q7. किसी आयत की लम्बाई में 10% की वृद्धि और चौड़ाई में 10% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
Ans. 1% की कमी।
Q8. किसी आयत की लम्बाई में 80% की वृद्धि और चौड़ाई में 50% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
Ans. 10% की कमी।
Q9. विरजन के उपरान्त एक तौलिए की लम्बाई में 20% की कमी और चौड़ाई में 10% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
Ans. 28% की कमी।
Q10. किसी आयत की लम्बाई में 50% की वृद्धि और चौड़ाई में 50% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
Ans. 25% की कमी।
Q11. किसी आयताकार खेत की लम्बाई में 70% की वृद्धि और चौड़ाई में 50% की कमी कर दी जाए तो उसके क्षेत्रफल में कितने % की वृद्धि या कमी होगी?
Ans. 15% की कमी।
Q12. एक आयताकार मैदान का परिमाप 480 मीटर हैं, इसकी लम्बाई और चौड़ाई का अनुपात 5 : 3 हैं बताइए उसका क्षेत्रफल कितना होगा?
Ans. 13,500
Q13. एक वृत्त की परिधि 352 सेमीमीटर हैं इसका क्षेत्रफल क्या होगा?
Ans. 9856 वर्ग सेमीमीटर
Q.14 56 सेमीमीटर व्यास वाले अर्द्ध गोलाकार का पतिमाप क्या होगा?
Ans. 144 सेमीमीटर
Q.15 एक पहिए का व्यास 1.26 मी. हैं यह 500 चक्कर में कितनी दूरी तय करेगी?
Ans. 1980
आशा है क्षेत्रमिति की जानकारी आपको पसंद आएगी और इस पोस्ट को पढ़कर आप क्षेत्रमिति के सूत्रों को समझकर प्रश्नो को हल करना सीख पाएंगे।
क्षेत्रमिति से संबंधित किसी भी प्रश्न के लिए कमेंट करे। यदि जानकारी पसंद आयी है तो पोस्ट को दोस्तों के साथ शेयर जरूर करे।


Mast hai aisa hi aur bhejo
Hello Kundan Pandey Ji,
यहाँ आप गणित के समस्त अध्याय पढ़ सकते है
समबाहु त्रिभुज के शीर्ष लम्ब की लंबाई ग़लत है
सुधार लीजिए
Hello RANJEET SAINI,
कृपया विस्तार में बताए क्या गलत है?
Thanks Sir
Nice Sir
Keep visiting Satyam.