इस पेज पर आप गणित विषय के महत्वपूर्ण अध्याय समबाहु त्रिभुज की जानकारी पढ़ेंगे।
पिछले पेज पर हमने त्रिभुज की जानकारी शेयर की है उसे जरूर पढ़े।
चलिए इस पेज पर समबाहु त्रिभुज की जानकारी को पढ़ते और समझते हैं।
समबाहु त्रिभुज किसे कहते हैं
जिस त्रिभुज की तीनो भुजाओं की लम्बाई बराबर होती है उसे समबाहु त्रिभुज कहते हैं।
समबाहु त्रिभुज के प्रत्येक कोण का मान 60° होता हैं।
समबाहु त्रिभुज के सूत्र
- समबाहु त्रिभुज का क्षेत्रफल = √3/4 × भुजा²
- समबाहु त्रिभुज का परिमाप = 3 × भुजा
- शीर्ष बिंदु से डाले गए लम्ब की लम्बाई = √3/4 × भुजा
- समबाहु त्रिभुज के अर्धवृत की त्रिज्या R = a/2 × √3
- परिवृत की त्रिज्या R = a/√3
समबाहु त्रिभुज के गुण
- समबाहु त्रिभुज की सभी भुजाएं आपस में समान होती हैं।
- समबाहु त्रिभुज के सभी अंतः कोण समान होते हैं।
- समबाहु त्रिभुज की प्रत्येक कोण का माप 60 डिग्री होता हैं।
- तीनों भुजाओं का योग 180 डिग्री के बराबर होता हैं।
- किसी भी भुजा पर डाला गया लम्ब सम्मुख कोण को समद्विभाजित करता हैं।
- शीर्ष से सम्मुख भुजा पर डाला गया लम्ब उस भुजा को समद्विभाजित करता हैं।
समबाहु त्रिभुज पर आधारित प्रश्न
Q.1 यदि किसी समबाहु त्रिभुज की एक भुजा 4√3 सेंटीमीटर हैं तो उसका क्षेत्रफल होगा?
A. 12/√3 वर्ग सेंटीमीटर
B. 24/√3 सेंटीमीटर
C. 12/√3 सेंटीमीटर
D. 21/√3 सेंटीमीटर
हल:- प्रश्नानुसार,
समबाहु त्रिभुज का क्षेत्रफल = √3/4 × (भुजा)²
क्षेत्रफल = √3/4 × (4√3)²
क्षेत्रफल = √3/4 × 16 × 3
क्षेत्रफल = 12√3 वर्ग सेंटीमीटर
Ans. 12√3 वर्ग सेंटीमीटर
Q.2 यदि एक समबाहु त्रिभुज के शीर्ष का मान √6 सेंटीमीटर हो, तो इसका क्षेत्रफल होगा?
A. 2√3 सेंटीमीटर²
B. 24/√3 सेंटीमीटर²
C. 12/√3 सेंटीमीटर²
D. 21/√3 सेंटीमीटर²
हल:- प्रश्नानुसार,
a² – a²/4 = 6
3a² = 6 × 4
a² = 8
a = √8
a = 2√2
समबाहु त्रिभुज का क्षेत्रफल = √3/4 × भुजा²
क्षेत्रफल = √3/4 × 8
क्षेत्रफल = 2√3 वर्ग सेंटीमीटर
Ans. 2√3 वर्ग सेंटीमीटर
Q.3 यदि किसी समबाहु त्रिभुज का क्षेत्रफल √3 सेंटीमीटर² हो, तो उसकी भुजा (सेंटीमीटर में) होगी?
A. 1 सेंटीमीटर
B. 2 सेंटीमीटर
C. 4 सेंटीमीटर
D. 5 सेंटीमीटर
हल:- प्रश्नानुसार,
क्षेत्रफल = √3
समबाहु त्रिभुज का क्षेत्रफल = √3/4 (भुजा)²
√3 = √3/4 (भुजा)²
√3/4 (भुजा)² = √3
(भुजा)² = √3 × 4/√3
(भुजा)² = 4
भुजा = √4
भुजा = 2
Ans. 2 सेंटीमीटर
Q.4 किसी समबाहु त्रिभुज का क्षेत्रफल 400√3 वर्ग मीटर हैं। तो इसका परिमाप हैं?
A. 120 मीटर
B. 150 मीटर
C. 90 मीटर
D. 135 मीटर
हल:- प्रश्नानुसार,
समबाहु त्रिभुज का क्षेत्रफल = √3/4 × (भुजा)²
400√3 = √3/4 × (भुजा)²
√3/4 (भुजा)² = 400√3
(भुजा)² = 4√3 × 400/√3
भुजा² = 4 × 400
भुजा² = 1600
भुजा = √1600
भुजा = 40
समबाहु त्रिभुज का परिमाप = 3 × भुजा
त्रिभुज का परिमाप = 3 × 40
परिमाप = 120
Ans. 120 मीटर
Q.5 एक समबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी एक भुजा का नाप 8 सेंटीमीटर हैं?
A. 55.424 c.m.²
B. 554.24 c.m.²
C. 5542.4 c.m.²
D. 55424 c.m.²
हल:- प्रश्नानुसार,
a = 8 c.m.
समबाहु त्रिभुज का क्षेत्रफल = √3/4 (भुजा)²
क्षेत्रफल = √3/4 × (8)²
क्षेत्रफल = √3 × 64/2
क्षेत्रफल = 1.732 × 32
क्षेत्रफल = 55.424 c.m.²
Ans. 55.424 c.m.²
Q.6 एक समबाहु त्रिभुज जिसका क्षेत्रफल 4√3 वर्ग सेंटीमीटर हैं इसकी भुजा हैं?
A. 1 सेंटीमीटर
B. 2 सेंटीमीटर
C. 3 सेंटीमीटर
D. 4 सेंटीमीटर
हल:- प्रश्नानुसार,
क्षेत्रफल = 4√3
समबाहु त्रिभुज का क्षेत्रफल = √3/4 (भुजा)²
4√3 = √3/4 (भुजा)²
√3/4 (भुजा)² = 4√3
(भुजा)² = 4√3 × 4/√3
भुजा² = 4 × 4
भुजा² = 16
भुजा = √16
भुजा = 4
Ans. 4 सेंटीमीटर
Q.7 समबाहु त्रिभुज का परिमाप ज्ञात कीजिये जिसकी भुजा का नाप 12 सेंटीमीटर हैं?
A. 12 सेंटीमीटर
B. 36 सेंटीमीटर
C. 48 सेंटीमीटर
D. 24 सेंटीमीटर
हल :- प्रश्नानुसार,
भुजा = 12 c.m.
समबाहु त्रिभुज का परिमाप = 3 × भुजा
परिमाप = 3 x 12
परिमाप = 36 सेंटीमीटर
Ans. 36 सेंटीमीटर
Q.8 किसी समबाहु त्रिभुज के अभ्यन्तर के किसी बिंदु से तीनों भुजाओं की लाम्बिक दूरियाँ √3 सेंटीमीटर, 2√3 सेंटीमीटर और 5√3 सेंटीमीटर हैं। इस त्रिभुज का परिमाप हैं। (सेंटीमीटर में)
A. 16
B. 34
C. 48
D. 24
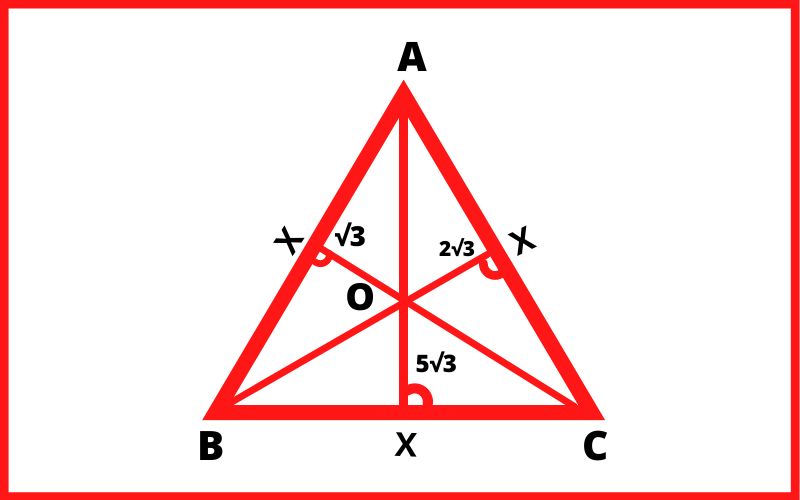
हल:- प्रश्नानुसार,
ABC का क्षेत्रफल = (AOB + AOC + BOC) का क्षेत्रफल
√3/4 x² = ½ × x × √3 + ½ × x × 2√3 + ½ × x × 5√3
= ½ x (√3 + 2√3 + 5√3)
x = 2/√3 × 8√3
x = 16
Ans. 16
Q.9 42 सेंटीमीटर की भुजा वाले एक समबाहु त्रिभुज के अंतः वृत्त का क्षेत्रफल होगा? (π = ²²⁄₇)
A. 231 सेंटीमीटर²
B. 462 सेंटीमीटर²
C. 22√3 सेंटीमीटर³
D. 924 सेंटीमीटर²
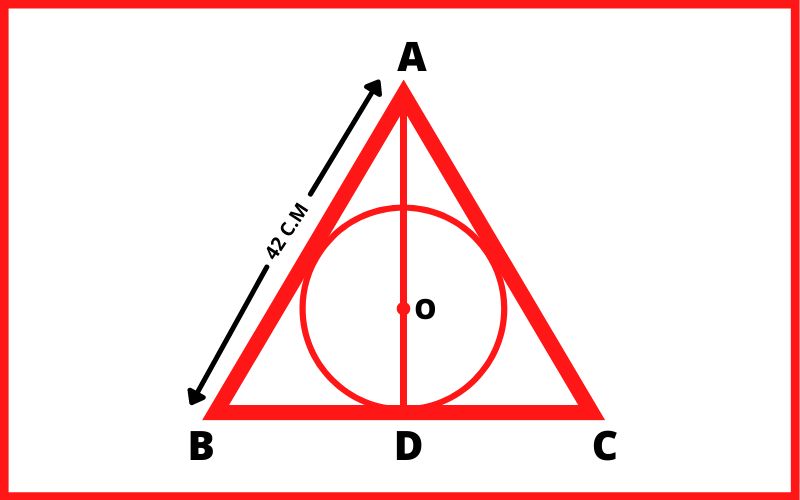
हल:- प्रश्नानुसार,
AD = √(42)² – (21)²
AD = √1764 – 441
AD = √1323 सेंटीमीटर
∴ OD = ⅓ √1323 सेंटीमीटर
अन्तः वृत्त का क्षेत्रफल = ²²⁄₇ × (⅓√1323)²
अन्तः वृत्त का क्षेत्रफल = ²²⁄₇ × ¹⁄₉ × 1323
अन्तः वृत्त का क्षेत्रफल = 22 × 21
अन्तः व्रत का क्षेत्रफल = 462 वर्ग सेंटीमीटर
Q.10 यदि एक समबाहु त्रिभुज की प्रत्येक भुजा उस व्रत की त्रिज्या के बराबर हैं। जिसका क्षेत्रफल 154 वर्ग सेंटीमीटर हैं तो समबाहु त्रिभुज का क्षेत्रफल क्या होगा?
A. 7√3 वर्ग सेंटीमीटर
B. 49√3/4 वर्ग सेंटीमीटर
C. 35 वर्गमीटर
D. 49 वर्ग सेंटीमीटर
हल:- प्रश्नानुसार,
πr² = 154
²²⁄₇ r² = 154
r² = 154 × ⁷⁄₂₂
r² = 7 × 7
r² = 49
r = √49
r = 7
त्रिभुज की भुजा = 7 सेंटीमीटर
समबाहु त्रिभुज का क्षेत्रफल = √3/4 × (भुजा)²
क्षेत्रफल = √3/4 × 49
क्षेत्रफल = 49√3/4 वर्ग सेंटीमीटर
जरूर पढ़िए :
उम्मीद हैं आपको समबाहु त्रिभुज की पोस्ट पसंद आयी होगी।
