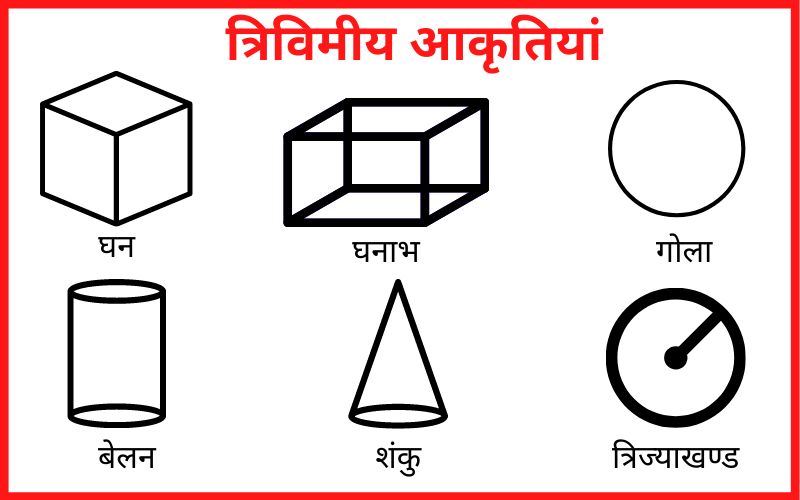
इस पेज पर हम क्षेत्रमिति के अंतर्गत त्रिविमीय आकृति के बारे में पड़ेगें। जिसमें घन, घनाभ, गोला, अर्द्धगोला, बेलन, शंकु, त्रिज्याखण्ड आदि को निकालना सीखेगें।
पिछले पेज पर हमने गणित विषय के महत्वपूर्ण अध्याय क्षेत्रमिति को शेयर किया हैं तो उसे जरूर पढ़े।
चलिए इस पेज पर त्रिविमीय आकृतियों के बारे में पढ़ते और समझते हैं।
त्रिविमीय आकृति किसे कहते है
त्रिविमीय आकृति के तीन आयाम होते हैं जैसे लंबाई, चौड़ाई और मोटाई। इसके आयतन, वक्र पृष्ठीय क्षेत्रफल, और कुल पृष्ठीय क्षेत्रफल की गणना की जा सकती हैं।
घन, घनाभ, गोला, बेलन, शंकु, त्रिज्याखण्ड आदि 3D आकृति के अंर्तगत आते हैं।
3D आकृतियां
घन
घन की लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं। एक घन में छः फलक, बारह किनारे एवं आठ कोने होते हैं इसके छह बराबर-बराबर आकार के फलक होते हैं हर फलक एक वर्ग होता हैं और छह फलक होने के कारण यह एक प्रकार का षट्फलकी भी कहलाता हैं।
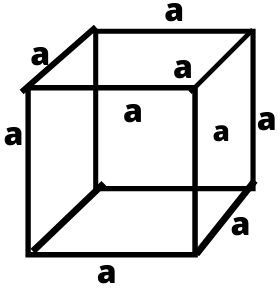
- घन का आयतन = a × a × a
- घन का परिमाप = 4 × a × a
- घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6 a² वर्ग सेंटीमीटर।
- घन का विकर्ण = √3a सेंटीमीटर।
घनाभ
छः पृष्ठों से घिरी वह आकृति, जिसमें प्रत्येक पृष्ठ एक आयत होता हैं और सम्मुख पृष्ठ बराबर होते हैं घनाभ कहलाती हैं।
घनाभ एक ऐसी त्रिआयामी (3d) आकृति है जिसके 6 आयताकार फलक होते हैं। इसी वजह से ऐसी आकृतियों को बहुफलक भी कहा जाता है।
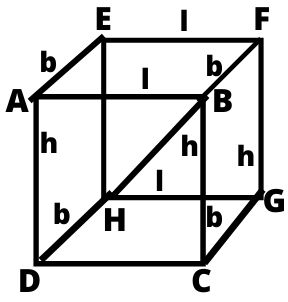
- घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
- घनाभ का आयतन = l × b × h
- घनाभ का परिमाप = 2(l + b) × h
- घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
- घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
- घनाभ के विकर्ण = √(लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
- घनाभ का विकर्ण = √l² + b² + h²
गोला
गोला वह ठोस है जिसमें केवल एक तल होता है और इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता है।
इस बिन्दु को गोले का केन्द्र कहते हैं तथा केन्द्र से गोले के किसी बिन्दु की दूरी को गोले की त्रिज्या कहते हैं।
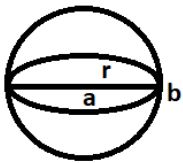
- गोला का आयतन = (4πr³)/3 घन सेंटीमीटर
- गोले का वक्र पृष्ठ = 4πr² वर्ग सेंटीमीटर
- अर्द्धगोले का आयतन = (2πr³)/3 घन सेंटीमीटर
- अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr² वर्ग सेंटीमीटर
- अर्द्वगोले की त्रिज्या r हो, तो
- अर्द्वगोले का आयतन = 2/3 πr³
- अर्द्वगोले का वर्कप्रष्ठ = 2πr²
- अर्द्वगोले का सम्पूर्ण पृष्ठ = 3πr²
बेलन
बेलन ज्यामिति में एक त्रिआयामी ठोस की आकृति है। इसका पार्श्व पृष्ठ वक्र, सिरे समान त्रिज्या के वृत्ताकार होते हैं, बेलन सरल रूप में एक रोलर या समान व्यास का गिलास है।
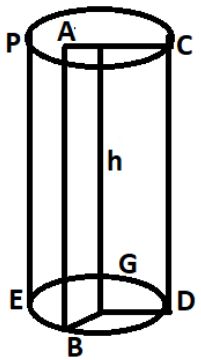
- बेलन का आयतन = πr²h
- बेलन के वक्र पृष्ठ का क्षेत्रफल = 2πrh
- बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल = (2πrh + 2πr²h) वर्ग सेंटीमीटर।
शंकु
शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
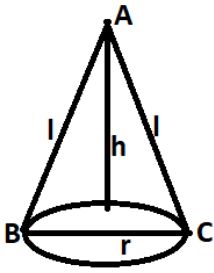
- L = √(r² + h²)
- शंकु का आयतन = (πr²h)/3 घन सेंटीमीटर।
- शंकु का वक्र पृष्ठ का क्षेत्रफल = πrl वर्ग सेंटीमीटर।
- शंकु का सम्पूर्ण पृष्ठ का क्षेत्रफल = (πrl + πr²) वर्ग सेंटीमीटर।
त्रिविमीय आकृतियों से संबंधित प्रश्न उत्तर
प्रश्न1. एक घनाभ की लम्बाई 15 मीटर, चौड़ाई 10 मीटर तथा ऊँचाई 4 मीटर हैं। इसका सम्पूर्ण प्रष्ठ हैं?
A. 420 वर्ग मी.
B. 450 वर्ग मी.
C. 500 वर्ग मी.
D. 600 वर्ग मी.
हल:- प्रश्ननानुसार,
घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
घनाभ का सम्पूर्ण प्रष्ठ = 2(15 × 10 + 10 × 4 + 4 × 15)
घनाभ का सम्पूर्ण प्रष्ठ = 2(150 + 40 + 60)
घनाभ का सम्पूर्ण प्रष्ठ = 2 × 250 वर्ग मीटर
उत्तर:- 500 वर्ग मीटर
प्रश्न2. किसी कमरे की चौड़ाई ऊँचाई की दूनी परन्तु लम्बाई की आधी हैं। कमरे का आयतन 512 घन मीटर हैं। कमरे की लम्बाई बताइए?
A. 12 मी.
B. 16 मी.
C. 32 मी.
D. 10 मी.
हल:- प्रश्ननानुसार,
माना ऊँचाई = h मीटर,
चौड़ाई = 2h मीटर
लम्बाई = 4h मीटर
आयतन = लम्बाई × चौड़ाई × ऊँचाई
512 = 4h × 2h × h
512 = 8h³
h³ = 512/8
h³ = 64
h = ∛64
h = 4
उत्तर:- 4 मीटर
प्रश्न3. एक घन का प्रत्येक किनारा 5 मीटर हैं, तो उसका कुल पृष्ठ क्षेत्रफल और आयत होगा?
A. 150 वर्ग मीटर, 125 घन मीटर
B. 25 वर्ग मीटर, 75 घन मीटर
C. 190 वर्ग मीटर, 175 घन मीटर
D. 40 वर्ग मीटर, 160 घन मीटर
हल:- प्रश्ननानुसार,
घन का कुल प्रष्ठ क्षेत्रफल = 6 × (भुजा)²
= 6 × 25
= 150 वर्ग मीटर
घन का आयतन = (भुजा)²
= (5)²
= 25
उत्तर:- 25 घन मीटर
प्रश्न4. एक बेलन का वृकप्रष्ठ 264 वर्ग मीटर हैं। उसका आयतन 924 घन मीटर हैं तो बेलन की ऊँचाई क्या होगीं?
A. 4 मीटर
B. 6 मीटर
C. 8 मीटर
D. 10 मीटर
हल:- प्रश्ननानुसार,
बेलन का वक्रप्रष्ठ = 2πrh
264 = 2 × 22/7 × rh
rh = 42
πr²h = 924
r = 7
h = 6
उत्तर:- 6 मीटर
प्रश्न5. दो शंकुओं के आयतन का अनुपात 2 : 3 हैं और उनके आधारों की त्रिज्याओं का अनुपात 1 : 2 हैं। उनकी ऊंचाइयों का अनुपात हैं?
A. 3 : 8
B. 8 : 3
C. 4 : 3
D. 3 : 4
हल:- प्रश्ननानुसार,
ऊंचाइयों का अभीष्ट अनुपात = 1/3π(R1)²h1/1/3π(R2)²h2
= 2/3
(1)²h1/4h2
2/3
h1/h2 = 2/3 × 4/1
= 8/3
उत्तर:- 8 : 3
प्रश्न6. यदि शंकु की ऊँचाई दुगुनी कर दी जाए तो उसका आयतन बढेगा?
A. 100%
B. 200%
C. 300%
D. 400%
हल:- प्रश्ननानुसार,
आयतन में प्रतिशत वृद्धि = [(1/3 πr² × 2h – 1/3 π²h)/(1/3πr²h)] × 100
उत्तर:- 100%
जरूर पढ़िए :
उम्मीद हैं आपको त्रिविमीय आकृति की जानकारी पसंद आयीं होगीं।
त्रिविमीय आकृति से संबंधित किसी भी प्रश्न के लिए कमेंट करें।