इस पेज पर आप गणित के महत्वपूर्ण अध्याय त्रिकोणमिति की समस्त जानकारी को पढ़कर समझेंगे।
पिछली पोस्ट में हम गणित के महत्वपूर्ण अध्याय क्षेत्रमिति की जानकारी शेयर कर चुके है उसे जरूर पढ़े।
चलिए आज हम इस पेज पर त्रिकोणमिति की परिभाषा, सूत्र और उदाहरण की समस्त जानकारी पढ़ते हैं।
त्रिकोणमिति किसे कहते हैं
त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच संबंधों का अध्ययन किया जाता है।
त्रिकोणमिति अंग्रेजी के शब्द ‘Trigonometry’ से मिलकर बना है।
Trigonometry शब्द तीन ग्रीक शब्दों Tri + Gon + Metron से मिलकर बना है।
- इनमें ‘Tri’ का अर्थ है ‘तीन’
- ‘Gon’ का अर्थ है ‘भुजा’ तथा
- ‘Metron’ का अर्थ होता है ‘माप’
अर्थात अंग्रेजी शब्द ‘Trigonometry’ का पूर्ण अर्थ – ‘त्रिभुज की तीनों भुजाओं की माप’ होता है।
समकोण त्रिभुज (Right Angle Triangle) :
जिस त्रिभुज में एक कोण 90o हो उसे समकोण त्रिभुज कहा जाता है।
एक समकोण त्रिभुज में एक समकोण तथा दो न्यून कोण (90o से कम का का कोण) होते हैं।
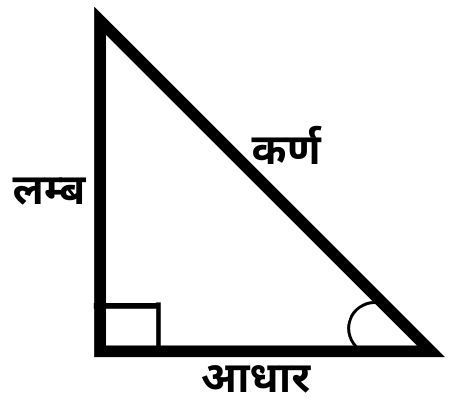
कर्ण (Hypotenuse)
- समकोण त्रिभुज में समकोण के सामने की भुजा को कर्ण कहा जाता है।
- कर्ण समकोण त्रिभुज की सबसे लम्बी भुजा होती है।
- कर्ण की लम्बाई शेष दोनों भुजाओं की लम्बाई के योग से कम होती है।
- कर्ण को प्राय: अंग्रेजी के अक्षर “h” से दिखलाया जाता है।
आधार (Base)
- समकोण त्रिभुज में एक न्यूनकोण की संलग्न भुजा को आधार कहा जाता हैं, आधार जैसा कि शब्द के अर्थ से ही स्पष्ट है, एक समकोण त्रिभुज में कर्ण को छोड़कर नीचे वाली भुजा जो आधार का कार्य करती है आधार कहलाती है।
- आधार को प्राय: अंग्रेजी के अक्षर “b” से निरूपित किया जाता है।
लम्ब (Perpendicular)
- समकोण त्रिभुज में किसी न्यूनकोण के सम्मुख की भुजा को लम्ब कहा जाता है।
- लम्ब को ऊँचाई भी कहा जाता है। लम्ब को प्राय: अंग्रेजी के अक्षर “p” से निरूपित किया जाता है।
पाइथागोरस प्रमेय (Pythagoras Theorem)
पाइथागोरस प्रमेय एक समकोण त्रिभुज की भुजाओं के बीच सम्बन्ध को दर्शाता है।
पाइथागोरस प्रमेय के अनुसार समकोण त्रिभुज में,
(कर्ण) 2 = (लम्ब) 2 + (आधार) 2
⇒ h2 = p2 + b2
जहाँ :
- h = कर्ण (Hypotenuse)
- p = लम्ब (perpendicular) तथा
- b = आधार (base)
समकोण त्रिभुज का नियम (Right Angle tringle’s Rule) :
(कर्ण)² = (लम्ब)² + (आधार)²
(लम्ब)² = (कर्ण)² – (आधार)²
(आधार)² =(कर्ण)² – (लम्ब)²
त्रिकोणमितीय अनुपात (Trigonometric Ratio):
त्रिकोणमितीय अनुपात 6 प्रकार के होते हैं जिन्हें निम्न प्रकार से परिभाषित किया जा सकता हैं।
sinA = लम्ब/कर्ण
cosA = आधार/कर्ण
tanA = लम्ब/आधार
cosecA = कर्ण/लम्ब
secA = कर्ण/आधार
cotA = आधार/लम्ब
त्रिकोणमिति सम्बन्ध (Trigonometric Relation) :
sinθ.cosecθ = 1
cosθ.secθ = 1
tanθ.cotθ = 1
tanθ = sinθ/cosθ
त्रिकोणमिति के सूत्र
- sin(A+B) = sinA.cosB+cosA.sinB
- sin(A-B) = sinA.cosB-cosA.sinB
- cos(A+B) = cosA.cosB-sinA.sinB
- cos(A-B) = cosA.cosB+sinA.sinB
- tan(A+B) = (tanA+tanB)/(1-tanA.tanB)
- tan(A-B) = (tanA-tanB)/(1+tanA.tanB)
- sin2A = 2sinA.cosA
- cos2A = cos2A-sin2A = 2cos2A-1 = 1-2sin2A
- tan2A = 2tanA/(1-tan2A)
त्रिकोणमिति सारणी
| θ | 0 | 30°= Π/6 | 45°= Π/4 | 60°= Π/3 | 90°= Π/2 | 180°= Π | 270°= 3Π/2 | 360°= 2Π |
|---|---|---|---|---|---|---|---|---|
| sinθ | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cosθ | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tanθ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cosecθ | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| secθ | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| cotθ | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
त्रिकोणमितीय की सर्वसमिकाएँ
- sin² A + cos² A = 1
- 1 + tan² A = sec² A
- 1 + cot² A = cosec² A
नीचे हम इन सर्वसमिकाओ को हल करेंगे।
sin² A + cos² A = 1
माना कि,
ABC एक समकोण त्रिभुज हैं, जिसमें त्रिभुज CAB = A, तब पाइथागोरस प्रमेय से,
(लम्ब²) + (आधार²) = (कर्ण²)
(BC)² + (AB)² = (AC)² ……………….(1)
समीकरण (1) के दोनों पक्षों में (AC)² से भाग देने पर,
(BC)² / (AC)² + (AB)² / (AC)² = (AC)² / (AC)²
(BC/AC)² + (AB/AC)² = (AC/AC)²
(Sin A = BC/AC), (Cos A = AB/AC)
sin²A + cos²A = 1 Prooved.
1 + tan² A = sec² A
माना कि,
ABC एक समकोण त्रिभुज हैं, जिसमें त्रिभुज CAB = A, तब पाइथागोरस प्रमेय से,
(लम्ब²) + (आधार²) = (कर्ण²)
(BC)² + (AB)² = (AC)² ……………….(1)
समीकरण (1) के दोनों पक्षों में (AB)² से भाग देने पर,
(BC)² / (AB)² + (AB)² / (AB)² = (AC)² / (AB)²
(BC/AB)² + (AB/AB)² = (AC/AB)²
1 + (tan²)A = (sec²)A Prooved.
1 + (cot²) = (cosec²)A
माना कि,
कि ABC एक समकोण त्रिभुज हैं, जिसमें त्रिभुज CAB = A, तब पाइथागोरस प्रमेय से,
(लम्ब²) + (आधार²) = (कर्ण²)
(BC)² + (AB)² = (AC)² ……………….(1)
समीकरण (1) के दोनों पक्षों में (BC)² से भाग देने पर,
(BC)² / (BC)² + (AB)² / (BC)² = (AC)² / (BC)²
(BC/BC)² + (AB/BC)² = (AC/BC)²
cot² A + 1 = cosec² A
1 + (cot²) = (cosec²) A Prooved.
पूरक कोणों में त्रिकोणमितीय अनुपात
| sin (90° – θ) | cos θ |
| cos (90° – θ) | sin θ |
| tan (90° – θ) | cot θ |
| cosec (90° – θ) | sec θ |
| sec (90° – θ) | cosec θ |
| cot (90° – θ) | tan θ |
| sin (90° + θ) | cos θ |
| cos (90° + θ) | – sin θ |
| tan (90° + θ) | – cot θ |
| cosec (90° + θ) | sec θ |
| sec (90° + θ) | – cosec θ |
| cot (90° + θ) | – tan θ |
| sin (180° – θ) | sin θ |
| cos (180° – θ) | – cos θ |
| tan (180° – θ) = | – tan θ |
| cosec (180° – θ) | cosec θ |
| sec (180° – θ) | – sec θ |
| cot (180° – θ) | – cot θ |
| sin (180° + θ) | – sin θ |
| cos (180° + θ) | – cos θ |
| tan (180° + θ) | tan θ |
| cosec (180° + θ) | – cosec θ |
| sec (180° + θ) | – sec θ |
| cot (180° + θ) | cot θ |
| sin (360° – θ) | – sin θ |
| cos (360° – θ) | cos θ |
| tan (360° – θ) | – tan θ |
| cosec (360° – θ) | – cosec θ |
| sec (360° – θ) | sec θ |
| cot (360° – θ) | – cot θ |
| sin (360° + θ) | sin θ |
| cos (360° + θ) | cos θ |
| tan (360° + θ) | tan θ |
| cosec (360° + θ) | cosec θ |
| sec (360° + θ) | sec θ |
| cot (360° + θ) | cot θ |
त्रिकोणमिति से संबंधित प्रश्न-उत्तर
1. यदि sin A = 5/13 हो तो cosA का मान ज्ञात कीजिए?
A. 11/13
B. 12/13
C. 9/7
D. 13/17
हल: प्रश्नानुसार
sin A = 5/13
(Sin²)A + (cos²)A = 1
(cos²)A = 1 – (5/13)²
(cos²)A = 1 – (25/169)
(cos²)A = (169 – 25)/169
(cos²)A = 144/169
cosA = √144/169
cosA = 12/13
Ans. 12/13
2. यदि sec A = 5/3 हो तो tanA का मान ज्ञात कीजिए?
A. 2/3
B. 3/5
C. 4/3
D. 7/5
हल:- प्रश्नानुसार,
दिया गया हैं
Sec A = 5/3
सर्वसमिका : 1 + tan² A = sec² A
1 + tan² A = (5/3)²
1 + tan² A = 25/9
tan² A = 25/9 – 1
tan² A = (25 – 9)/9
tan² A = 16/9
tan² A = √16/9
tan² A = 4/3
Ans. 4/3
3. यदि sinA = 3/5 हो तो cotA का मान ज्ञात कीजिए?
A. 2/3
B. 3/5
C. 4/3
D. 3/7
हल:- प्रश्नानुसार,
दिया गया हैं
sin A = 3/5
सर्वसमिका : 1 + cot² = cosec²
1 + cot² A = 1/sin² A
1 + cot² A = 1/(3/5)²
1 + cot² A = 1 / 9/25
1 + cot² A = 1/1 × 25/9
1 + cot² A = 25/9
cot² A = 25/9 – 1
cot² A = (25 – 9)/9
cot² A = 16/9
cot² A = 4/3
Ans. 4/3
4. 120° को रेडियन में व्यक्त कीजिए?
A. 4π/3 रेडियन
B. 2π/3 रेडियन
C. 5π/2 रेडियन
D. π/3 रेडियन
हल: प्रश्नानुसार
180° = π रेडियन
1° = π/180° रेडियन
120° = (π × 120°)/180°
= 2π/3 रेडियन
Ans. 2π/3 रेडियन
5. 3π/2 रेडियन को अंश में व्यक्त कीजिए?
A. 250°
B. 270°
C. 230°
D. 370°
हल: प्रश्नानुसार
π रेडियन = 180″°
1 रेडियन = 180°/π
3π/2 रेडियन = (180°π × 3π)/(π × 2)
= 90° × 3
= 270°
Ans. 270°
6. सिद्ध कीजिए कि 2 sin^2 A + cos^4 A = 1 + sin^4 A
A. 1 + cos^2 A
B. 2 + cos^4 A
C. 1 + sin^2 A
D. 1 + sin^4 A
हल:- प्रश्नानुसार,
बायाँ पक्ष = 2 sin^2 A + cos^4 A
= 2 sin^2 A + (1 – sin^2 A)^2
= 2 sin^2 A + 1 + sin^4 A – 2 sin^2 A
1 + sin^4 A (दायाँ पक्ष)
Ans. 1 + sin^4 A
7. यदि cosθ = 1/3 हो, तो sinθ + tanθ का मान होगा?
A. 8√2/3
B. 4√5/3
C. 3√2/7
D. 11√3/9
हल:- प्रश्नानुसार,
cosθ = आधार/कर्ण
cosθ = 1/3
लम्ब = √(कर्ण)² – (आधार)²
लम्ब = √(3)² – (1)²
लम्ब = √(9 – 1)
लम्ब = √8
लम्ब = 2√2
sinθ + tanθ = लम्ब/कर्ण + लम्ब/आधार
sinθ + cosθ = 2√2/3 + 2√2/1
sinθ + cosθ = (2√2/3 + 6√2)/3
sinθ + cosθ = 8√2/3
Ans. 8√2/3
8. यदि cosθ = m/n हो, तो tanθ का मान होगा?
A. √(n³ – m³)/m
B. √(m² – n²)/n
C. √(n³ – m³)/N
D. √(n² – m²)/m
हल:- प्रश्नानुसार,
cosθ = आधार/कर्ण
cosθ = m/n
लम्ब = √(n² – m²)
tanθ = लम्ब/आधार
tanθ = √(n² – m²)/m
Ans. √(n² – m²)/m
9. tan 15°. tan 25°. tan 45°. tan 65°. tan 75° का मान हैं?
A. √3
B. √2
C. 1
D. 0
हल:- प्रश्नानुसार,
tan 15°. tan 25°. tan 45°. tan 65°. tan 75°
tan (90° – 75°) . tan (90° – 65°) . tan 45 . tan 65° . tan 75°
cot 75° . cot 65° . tan 45° . tan 65° . tan 75°
tan 45° = 1
Ans. 1
10. यदि a = sin (π/4), b = cos (π/4) तथा c = – cosec (π/4) हो, तो a³ + b³ + c³ का मान हैं?
A. -4/3√2
B. √5/7
C. 3/√2
D. -3/2√2
हल:- प्रश्नानुसार,
a + b + c = sin (π/4) + cos (π/4) – cosec (π/4)
a + b + c = 1/√2 + 1/√2 – √2 = 0
यदि a+ b + c = 0 हो, तो
a³ + b³ + c³ = 3abc
a³ + b³ + c³ = 3 sin (π/4) × cos (π/4) × {-cosec (π/4)}
a³ + b³ + c³ = 3 × 1/√2 × 1/√2 × (-√2)
a³ + b³ + c³ = 3 × 1/2 × (-√2)
a³ + b³ + c³ = – 3/2 √2
Ans. -3/2√2
11. यदि tan (A + B) = 1/2 एवं tan (A – B) = 1/3, तो tan2A का मूल्य हैं?
A. 1
B. 2
C. √2
D. 4
हल:- प्रश्नानुसार,
दिया गया हैं
tan (A + B) = ½
A + B = tan^-1 (½) ………(1)
तथा tan (A – B) = 1/3
A – B = tan^-1 (1/3)………..(2)
समीकरण (1) तथा (2) को जोड़ने पर,
tan 2 A = 1
Ans. 1
12. Sin60° tan30° cos45° का मान ज्ञात कीजिए?
A. ¼
B. ½√2
C. √2/3
D. 2/√3
हल:- प्रश्नानुसार,
Sin60° का मान = √3/2
tan30° का मान = 1/√3
cos45° का मान = 1/√2
= Sin60° tan30° cos45°
= √3/2 × 1/√3 × 1/√2
= ½√2
Ans. ½√2
13. (cosθ + sinθ)² + (cosθ – sinθ)² बराबर हैं?
A. 1
B. 2
C. 4
D. √3
हल:- प्रश्नानुसार,
(cosθ + sinθ)² + (cosθ – sinθ)²
cos²θ + sin²θ + 2sinθcosθ + cos²θ + sin²θ – 2cosθsinθ
1 + 1 = 2
Ans. 2
14. sin (π/18) × (5π/18) × (7π/18) = ?
A. 1/2
B. 1/4
C. 3/2
D. 1/8
हल:- प्रश्नानुसार,
sin (π/18) × (5π/18) × (7π/18)
cos (π/2 – π/18) × cos (π/2 – 5π/18) × cos (π/2 – 7π/18)
cos4π/9 cos2π/9 cosπ/9 = sin [2³ . π/9]/2³ . sin π/9
(½)³ . sin8π/9/sinπ/9
1/8 . sin8π/9/sinπ/9
1/8 sin (π – π/9)/sin π/9
1/8 . (sin π/9/sin π/9)
1/8 × 1
1/8
Ans. 1/8
15. यदि tan² 45° – cos² 60° = x sin² 45° tan 60° हो तो x का मान बताए?
A. √3/4
B. ¼
C. √3/2
D. 4/√3
हल:- प्रश्नानुसार,
tan² 45° – cos² 60° = x sin² 45° tan 60°
(1)² – (½)² = x (1/√2)² (√3)
1 – (1/4) = x (½)√3
(4 – 1)/4 = √3/2 x
3/4 × 2/√3 = x
x = 3/2√3
x = 3√3/2×3
x = √3/2
Ans. √3/2
16. sin 75° का मान हैं?
A. (√3 + 1)/2√2
B. (√3 + 3)/4√3
C. (√2 + 1)/2√5
D. (√3 + 2)/3√2
हल:- प्रश्नानुसार,
sin 75° = sin (45° + 30°)
sin (A + B) =sin A cos B + cos A sin B
sin 45° cos 30° + cos 45° sin 30°
½ × √3/2 + 1/√2 × ½
√3/2√2 + ½√2
(√3 + 1)/2√2
Ans. (√3 + 1)/2√2
17. सिद्ध कीजिए कि sinA/(1 + cos A) + (1 + cosA)/sinA = 2 cosecA
हल: प्रश्नानुसार
बायाँ पक्ष = sinA/(1 + cos A) + (1 + cosA)/sinA
= sin² A + (1 + cos² A)² / sin A (1 + cos A)
= (sin² A + 1 + 2cos A + cos² A) / sin A (1 + cos A)
= (1 + 1 + 2 cosA) / sinA(1 + cosA)
= (2 + 2 cosA)/sinA(1 + cosA)
= 2(1 + cosA)/sinA(1 + cosA)
= 2/sinA
2cosecA (दायाँ पक्ष)
Ans. 2cosecA
18. सिद्ध कीजिए कि √(1 – sin A)/(1 + sin A) = sec A – tan A
हल: प्रश्नानुसार
करणी चिन्ह के अंदर के अंश और हर में 1 – sin A का गुणा करने पर
बायाँ पक्ष = √(1 – sin A)/(1 + sin A)
= √(1 – sin A) × (1 – sin A)/(1 + sin A) × (1 – sin A)
= √(1 – sin A)² / (1 – sin² A)
= 1 – sin A / √cos² A
= (1 – sin A)/cos A
= 1/coa A – sin A/cos A
sec A – tan A (दायाँ पक्ष)
Ans. sec A – tan A
19. (tan A + sec A – 1)/(tan A – sec A + 1) = (1 + sin A)/cos A = sec A + tan A
हल: प्रश्नानुसार
बायाँ पक्ष = (tan A + sec A – 1)/(tan A – sec A + 1)
= (tan A + sec A – 1) × (sec A + tan A) / (tan A – sec A + 1) × (sec A + tan A)
= (tan A + sec A – 1)(sec A + tan A) / (tan A – sec A) × (sec A + tan A) × (sec A + tan A)
= (tan A + sec A – 1)(sec A + tan A) / (tan² A – sec² A) + sec A + tan A
= (tan A + sec A – 1)(sec A + tan A) / -1 + sec A + tan A [ sec² A = 1 + tan² A]
= (tan A + sec A – 1)(sec A + tan A) / (tan A + sec A – 1)
= sec A + tan A
= 1/cos A + sin A/cos A
(1 + sin A)/cos A (दायाँ पक्ष)
Ans. (1 + sin A)/cos A
20. सिद्ध कीजिए कि (sin A + cos A)(tan A + cot A) = sec A + cosec A
हल: प्रश्नानुसार
बायाँ पक्ष = (sinA + cosA)(tanA + cotA)
= (sinA + cosA) (sinA/cosA + cosA/sinA)
= (sinA + cosA)(sin² A + cos² A)/cos A sin A
= sin A/(sin A cos A) + cos A/(sin A cos A)
= 1/cos A + 1/sin A
sec A + cosec A
Ans. sec A + cosec A
आशा है त्रिकोणमिति की जानकारी आपको पसंद आयी होगी।
त्रिकोणमिति से संबंधित किसी भी प्रश्न के लिए Comment करे।


Yr to h mere pass h pr or dusra ni h kya sir………
Nice post
Thank you.
Your feedback to thanks
🙂 Keep visiting
Tnks
🙂
aap ke is article ki help se sabhi math ke students ko bahut help milegi aap ke likhne ka trika bhi bahut hi acha hai and aap ke blog pe aur bhi bahut hi ache articels hai
Feedback ke liye thanks
Keep visiting
Thanks feedback ke liye
Keep visiting