इस पेज पर आप गणित विषय के महत्वपूर्ण अध्याय आयत की जानकारी पढ़ने वाले हैं।
पिछले पेज पर हमने त्रिभुज और चतुर्भुज की जानकारी शेयर की हैं आप उस पोस्ट को भी पढ़े।
चलिए आज हम आयत की समस्त जानकारी को पढ़ते और समझते हैं।
आयत किसे कहते हैं
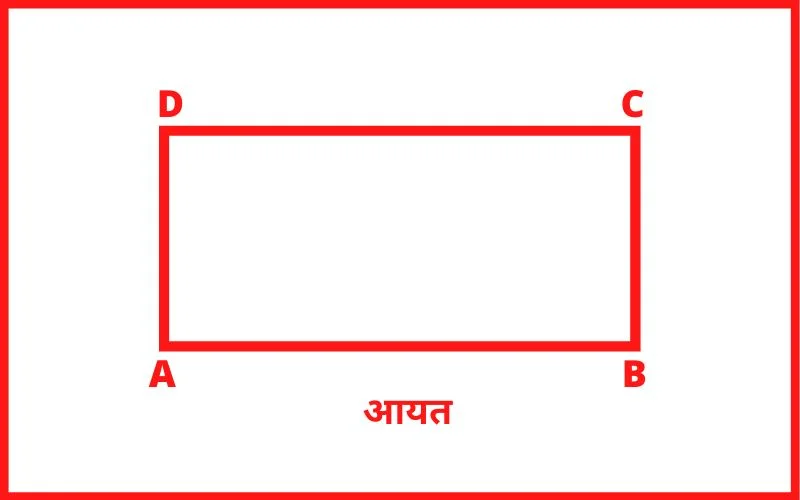
चार भुजाओं से घिरी वह आकृति, जिसमें आमने-सामने की भुजाएँ समान्तर और बराबर हो तथा प्रत्येक कोण समकोण हो उसे आयत कहते हैं।
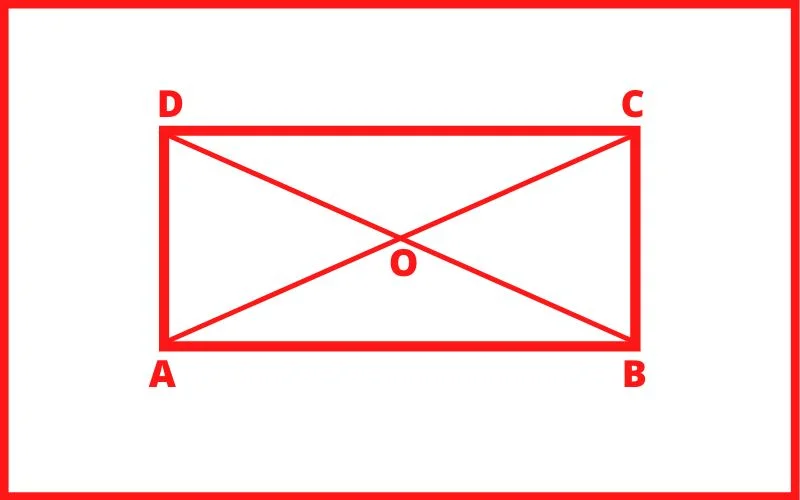
AC तथा BD को विकर्ण कहते हैं तथा ये आपस में बराबर होते हैं अर्थात AC = BD
आयत के सूत्र
आयत का परिमाप = 2(लम्बाई + चौड़ाई)
आयत का क्षेत्रफल = लंबाई × चौड़ाई
आयत का विकर्ण = √(लंबाई² + चौड़ाई²)
आयत से सम्बंधित महत्वपूर्ण बिंदु
- जब किसी आयत में एक विकर्ण डाला जाए तो उसमें बने दो त्रिभुज के क्षेत्रफल समान होगें।
- जब आयत में दो विकर्ण डाले जाए तो दोनों की लम्बाई समान होगी और आमने सामने के कोण भी समान होगे।
- जब किसी आयत के अंदर बड़े से बड़े वृत्त को बनाया जाए तब आयत की चौड़ाई वृत्त के व्यास के बराबर होती हैं।
- अन्तः वृत्त का क्षेत्रफल (πb²/ 4) होता हैं।
- जब आयत के बाहर की तरफ वृत्त बना हो तब आयत का विकर्ण वृत्त के व्यास के बराबर होता हैं।
Case#1.
आयत की चौड़ाई = वृत का व्यास
चौड़ाई/2 = वृत्त की त्रिज्या
b/2 = r
r = b/2
दोनों पक्षों का वर्ग करके π से गुणा करने पर
πr² = π(b/2)²
आयत के अन्तः वृत्त का क्षेत्रफल = (πb²)/4
Case#2.
आयत के विकर्ण = वृत्त का व्यास
विकर्ण/2 = वृत्त की त्रिज्या
r = D/2
दोनों पक्षों का वर्ग करने पर
π r² = π (D/2)²
आयत के बाह्य वृत का क्षेत्रफल = (πD²)/4
Case#3.
आंतरिक वृत और बह्यवृत के अनुपातों का क्षेत्रफल
आंतरिक वृत : बह्यवृत
त्रिज्या का अनुपात = b : d
परिधि का अनुपात = b : d
क्षेत्रफल का अनुपात = b² : d²
Note :-
जब किसी आयत के अंतवृत और बाह्यवृत्त के संबंधों का अनुपात दर्शाया जाए।
त्रिज्या और परिधि के अनुपात हमेशा समान होगें, इनके वर्ग करने पर क्षेत्रफल का अनुपात प्राप्त हो।
आयत की चौथाई और विकर्ण ही अंतवृत और बह्यवृत की त्रिज्या और परिधि के अनुपात होते हैं।
आयत के प्रश्न उत्तर
प्रश्न1. यदि किसी आयत की लम्बाई 5 सेंटीमीटर और चौड़ाई 7 सेंटीमीटर हो तो आयत का परिमाप क्या होगा?
A. 10 सेंटीमीटर
B. 14 सेंटीमीटर
C. 24 सेंटीमीटर
D. 28 सेंटीमीटर
हल:- दिया है.
लम्बाई a = 5 सेंटीमीटर
चौड़ाई b = 7 सेंटीमीटर
आयत का परिमाप = 2 (a + b)
P = 2 (5 + 7)
p = 2 × 12
P = 24 सेंटीमीटर
Ans. 24 सेंटीमीटर
प्रश्न2. यदि किसी आयत की लम्बाई एवं चौड़ाई क्रमशः 4 सेंटीमीटर और 12 सेंटीमीटर हो तो आयत का परिमाप क्या होगा?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 28 सेंटीमीटर
D. 32 सेंटीमीटर
हल:- दिया है.
लम्बाई a = 4 सेंटीमीटर
चौड़ाई b = 12 सेंटीमीटर
आयत का परिमाप = 2 (a + b)
P = 2 (4 + 12)
p = 2 × 16
P = 32 सेंटीमीटर
Ans. 32 सेंटीमीटर
प्रश्न3. यदि किसी आयत का परिमाप 24 सेंटीमीटर तथा लम्बाई 4 सेंटीमीटर हो, तो आयत की चौड़ाई निकालिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 32 सेंटीमीटर
D. 40 सेंटीमीटर
हल:- प्रश्नानुसार,
परिमाप = 24 सेंटीमीटर
लम्बाई = 4 सेंटीमीटर
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
24 = 2 (4 + चौड़ाई)
24/2 = 4 + चौड़ाई
12 = 4 + चौड़ाई
12 – 4 = चौड़ाई
चौड़ाई = 8 सेंटीमीटर
प्रश्न4. यदि किसी आयत का परिमाप 48 सेंटीमीटर तथा लम्बाई 12 सेंटीमीटर हो, तो आयत की चौड़ाई निकालिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 32 सेंटीमीटर
D. 40 सेंटीमीटर
हल:- प्रश्नानुसार,
परिमाप = 48 सेंटीमीटर
लम्बाई = 12 सेंटीमीटर
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
48 = 2 (12 + चौड़ाई)
48/2 = 12 + चौड़ाई
24 = 12 + चौड़ाई
24 – 12 = चौड़ाई
चौड़ाई = 12 सेंटीमीटर
प्रश्न5. यदि किसी आयत का परिमाप 32 सेंटीमीटर तथा चौड़ाई 8 सेंटीमीटर हो, तो आयत की लम्बाई निकालिए?
A. 2 सेंटीमीटर
B. 4 सेंटीमीटर
C. 6 सेंटीमीटर
D. 8 सेंटीमीटर
हल:- प्रश्नानुसार,
परिमाप = 32 सेंटीमीटर
चौड़ाई = 8 सेंटीमीटर
लम्बाई = ?
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
32 = 2 (लम्बाई + 8)
32/2 = लम्बाई + 8
16 = लम्बाई + 8
16 – 8 = लम्बाई
लम्बाई = 8 सेंटीमीटर
Ans. 8 सेंटीमीटर
प्रश्न6. यदि किसी आयत का परिमाप 56 सेंटीमीटर तथा चौड़ाई 18 सेंटीमीटर हो, तो आयत की लम्बाई निकालिए?
A. 8 सेंटीमीटर
B. 10 सेंटीमीटर
C. 12 सेंटीमीटर
D. 20 सेंटीमीटर
हल:- प्रश्नानुसार,
परिमाप = 56 सेंटीमीटर
चौड़ाई = 18 सेंटीमीटर
लम्बाई = ?
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
56 = 2 (लम्बाई + 18)
56/2 = लम्बाई + 18
28 = लम्बाई + 18
28 – 18 = लम्बाई
लम्बाई = 10 सेंटीमीटर
Ans. 10 सेंटीमीटर
प्रश्न7. एक आयताकार मैदान की लंबाई और चौड़ाई का अनुपात 4 : 3 हैं यदि मैदान का क्षेत्रफल 732 मीटर² हो तो मैदान के चारों और तीन बार लपेटने में कुल कितना तार लपेटना पड़ेगा?
A. 150 मीटर
B. 240 मीटर
C. 241 मीटर
D. 336 मीटर
हल:- आयताकार मैदान की लंबाई = 4x मीटर
तथा आयताकार मैदान की चौड़ाई = 3x मीटर
आयताकार मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
768 = (4x) × (3x)
768 = 12 x²
x² = 768/12
x² = 64
x = √64
x = 8 मीटर
अतः लम्बाई = 4x
4 × 8 = 32 मीटर
तथा चौड़ाई = 3x
3 × 8 = 24 मीटर
आयताकार मैदान का परिमाप = 2 (लम्बाई + चौड़ाई)
= 2(32 + 24)
= 2 × 56
= 112 मीटर
अतः तीन चक्कर में लपेटा गया कुल तार = 3 × परिमाप
= 3 × 112
Ans. 336 मीटर
प्रश्न8. एक आयत की लम्बाई 15 सेंटीमीटर और इसके विकर्ण की लम्बाई 17 सेंटीमीटर हो तो आयत का क्षेत्रफल कितना होगा?
A. 120 वर्ग सेंटीमीटर
B. 220 वर्ग सेंटीमीटर
C. 60 वर्ग सेंटीमीटर
D. 180 वर्ग सेंटीमीटर
हल:- विकर्ण = 17 सेंटीमीटर
लम्बाई = 15 सेंटीमीटर
आयत का विकर्ण =√(l² + b²)
17 = √l² + (15)²
(17)² = l² + (15)²
(17)² – (15)² = l²
289 – 225 = l²
l² = 64
l = 8
आयत का क्षेत्रफल = l × b
= 8 × 15
Ans. 120 वर्ग सेंटीमीटर।
प्रश्न9. एक आयत का क्षेत्रफल 252 वर्ग सेंटीमीटर हैं। इसकी लम्बाई तथा चौड़ाई 9 : 7 हैं, इसका परिमाप क्या हैं?
A. 87 सेंटीमीटर
B. 56 सेंटीमीटर
C. 87 सेंटीमीटर
D. 64 सेंटीमीटर
हल:- आयत का क्षेत्रफल = 252
लम्बाई = 9
चौड़ाई = 7
9x × 7x = 252
63x² = 252
x² = 4
x = 2
9 × 2 = 18
7 × 2 = 14
आयत का परिमाप = 2(l + b)
= 2(18 + 14)
= 2 × 32
= 64
Ans. 64 सेंटीमीटर
प्रश्न10. एक आयताकार खेत के चारों और अंदर से सीमा से लगा हुआ 8 मीटर चौड़ा रास्ता बना हैं यदि खेत को लम्बाई और चौड़ाई क्रमशः 220 मीटर और 180 मीटर हो तो रास्ता का क्षेत्रफल क्या होगा?
A. 2,014 वर्ग मीटर
B. 3,024 वर्ग मीटर
C. 4,879 वर्ग मीटर
D. 6,144 वर्ग मीटर
हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 220 × 180
= 39,600 वर्ग मीटर
लम्बाई = 220 – 16
लम्बाई = 204
चौड़ाई = 180 – 16
चौड़ाई = 164
क्षेत्रफल = लम्बाई × चौड़ाई
= 204 × 164
= 33,456 वर्ग मीटर
रास्ते का क्षेत्रफल = 39,600 – 33,456
= 6,144
Ans. 6,144 वर्ग मीटर।
FAQ
उत्तर :- आयत एक ऐसी आकृति है जिसमें चार सीधी भुजाएँ और चार समकोण होते हैं।
उत्तर :- आयत चार भुजाओं वाली आकृति होती है जिसमें चार समकोण (90 डिग्री कोण) होते हैं। वर्ग और फिबोनाची आयत सहित दो प्रकार के विशेष आयत होते हैं ।
उत्तर :- ऐसा चतुर्भुज जिसके चारों अन्तःकोण समकोण (= 90° के) हों उसे आयत (Rectangle) कहते हैं। आयत एक ऐसा चतुर्भुज है जिसकी आमने सामने की भुजाएं समांतर होती है, “आयत” कहलाता है।
उत्तर :- आयत की परिधि की गणना करने का सूत्र P = 2l + 2w है, जहाँ P आयत की परिधि हैl
इसकी लंबाई है, और w इसकी चौड़ाई है, सभी को इकाइयों में मापा जाता है। आयत का क्षेत्रफल ज्ञात करने का सूत्र A = lxw है।
जहाँ A वर्ग इकाई में आयत का क्षेत्रफल है, तथा l और w आयत की लम्बाई और चौड़ाई इकाई में हैं।
उत्तर :- आयत एक प्रकार का चतुर्भुज है जिसकी समांतर भुजाएँ एक दूसरे के बराबर होती हैं और सभी चार शीर्ष 90 डिग्री के बराबर होते हैं।
जरूर पढ़िए :
उम्मीद हैं आपको आयत की जानकारी पसंद आयी होगीं यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ जरूर शेयर करें।
यदि आप आयत से सम्बंधित किसी भी प्रकार का प्रश्न पूछना चाहते हो तो कमेंट में जरूर पूछें धन्यवाद।

आयत के सूत्र बताइए समझ के भाई साहब प्लीज लाइक
आर्टिकल में आयत के सूत्र दिए गए है