इस पेज पर आप गणित विषय के महत्वपूर्ण अध्याय वर्गमूल एवं घनमूल की को विस्तार से पड़कर समझेंगे।
पिछले पेज पर हम गणित विषय के महत्वपूर्ण अध्याय त्रिकोणमिति की समस्त जानकारी शेयर कर चुके है उसे अवश्य पढ़े।
चलिए वर्गमूल और घनमूल की समस्त जानकारी को पढ़ना शुरू करते है।
वर्गमूल
किसी संख्या का वर्गमूल वह संख्या होती हैं जिसे परस्पर दो बार गुणा करने पर दी गई संख्या प्राप्त होती हैं। इसे (√) चिन्ह से दर्शाते हैं।
जैसे:-
25 का वर्गमूल = √25 = 5
49 का वर्गमूल = √49 = 7
81 का वर्गमूल = √81 = 9
वर्गमूल निकालने का तरीका
(A). गुणनखण्ड विधि
किसी संख्या के अभाज्य गुणनखण्डों के प्रत्येक जोड़े में से एक लेकर इनका गुणनफल ही संख्या का वर्गमूल होगा।
जैसे:- 625 का वर्गमूल ज्ञात?
हल:- 625 = 5 × 5 × 5 × 5
625 =5^2 × 5^2
√625 = 5 × 5
√625 = 25
(B) भाग विधि
इस विधि में संख्या में दाईं ओर से दो-दो अंकों का जोड़ा बनाकर वर्गमूल मालूम करते हैं।
जैसे:- 50625 का वर्गमूल ज्ञात कीजिए?
हल:- √50625 = 225
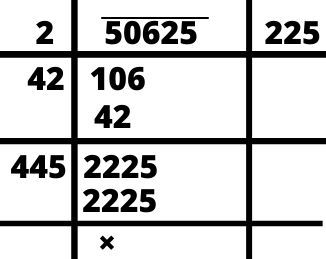
नोट:- यदि किसी संख्या में इकाई के स्थान पर 2, 3, 7 या 8 हो तो उस संख्या का वर्गमूल पूरा-पूरा नहीं निकलेगा।
वर्गमूल निकालने के लिए महत्वपूर्ण बिन्दु
- दाई ओर से दो अंको का जोड़ा बनाये और शेष बचे सभी अंको का एक जोड़ा बनाये।
- संख्या में दिया इकाई किसी संख्या का वर्गमूल करने पर प्राप्त होगी यह पता लगाएं और उसे उत्तर में सबसे अंत में लिखे।
- शेष अंको के जोड़े से बनी हुई संख्या के सबसे नजदीक आने वाली ऐसी संख्या जिस संख्या का वर्ग हो उसे उत्तर में बाई ओर लिखे।
- यदि ऐसी स्थिति में दो संख्या प्राप्त हो तो उनके बीच इकाई अंक 5 वाली संख्या का वर्ग करके दी गई संख्या से तुलना करें, तुलना करने पर दी गई संख्या छोटी संख्या हैं, तो उत्तर छोटा होगा और दी गई संख्या तुलना करने पर बड़ी संख्या प्राप्त हो तो उत्तर बड़ा होगा।
1 से लेकर 100 तक के वर्गमूल
| √1 | 1 |
| √4 | 2 |
| √9 | 3 |
| √16 | 4 |
| √25 | 5 |
| √36 | 6 |
| √49 | 7 |
| √64 | 8 |
| √81 | 9 |
| √100 | 10 |
| √121 | 11 |
| √144 | 12 |
| √169 | 13 |
| √196 | 14 |
| √225 | 15 |
| √256 | 16 |
| √289 | 17 |
| √324 | 18 |
| √361 | 19 |
| √400 | 20 |
| √441 | 21 |
| √484 | 22 |
| √529 | 23 |
| √576 | 24 |
| √625 | 25 |
| √676 | 26 |
| √729 | 27 |
| √784 | 28 |
| √841 | 29 |
| √900 | 30 |
| √961 | 31 |
| √1024 | 32 |
| √1089 | 33 |
| √1156 | 34 |
| √1225 | 35 |
| √1296 | 36 |
| √1369 | 37 |
| √1444 | 38 |
| √1521 | 39 |
| √1600 | 40 |
| √1681 | 41 |
| √1764 | 42 |
| √1849 | 43 |
| √1936 | 44 |
| √2025 | 45 |
| √2116 | 46 |
| √2209 | 47 |
| √2304 | 48 |
| √2401 | 49 |
| √2500 | 50 |
| √2601 | 51 |
| √2704 | 52 |
| √2809 | 53 |
| √2916 | 54 |
| √3025 | 55 |
| √3136 | 56 |
| √3249 | 57 |
| √3364 | 58 |
| √3481 | 59 |
| √3600 | 60 |
| √3,721 | 61 |
| √3,844 | 62 |
| √3,969 | 63 |
| √4,096 | 64 |
| √4,225 | 65 |
| √4,356 | 66 |
| √4,489 | 67 |
| √4,624 | 68 |
| √4,761 | 69 |
| √4,900 | 70 |
| √5,041 | 71 |
| √5,184 | 72 |
| √5,329 | 73 |
| √5,476 | 74 |
| √5,625 | 75 |
| √5,776 | 76 |
| √5,929 | 77 |
| √6,084 | 78 |
| √6,241 | 79 |
| √6,400 | 80 |
| √6,561 | 81 |
| √6,724 | 82 |
| √6,889 | 83 |
| √7,056 | 84 |
| √7,225 | 85 |
| √7,396 | 86 |
| √7,569 | 87 |
| √7,744 | 88 |
| √7,921 | 89 |
| √8,100 | 90 |
| √8,281 | 91 |
| √8,464 | 92 |
| √8,649 | 93 |
| √8,836 | 94 |
| √9,025 | 95 |
| √9,216 | 96 |
| √9,409 | 97 |
| √9,604 | 98 |
| √9,801 | 99 |
| √10,000 | 100 |
1 से लेकर 15 तक कि संख्याओं का वर्गमूल
| √1 | 1 |
| √2 | 1.41421… |
| √3 | 1.73205… |
| √4 | 2 |
| √5 | 2.23606… |
| √6 | 2.449… |
| √7 | 2.646… |
| √8 | 2.828… |
| √9 | 3 |
| √10 | 3.162… |
| √11 | 3.317… |
| √12 | 3.464… |
| √13 | 3.606… |
| √14 | 3.714… |
| √15 | 3.873… |
दशमलव संख्याओं के वर्गमूल
| √.1 | 0.32 |
| √.2 | 0.45 |
| √.3 | 0.55 |
| √.4 | 0.63 |
| √.5 | 0.71 |
| √.6 | 0.77 |
| √.7 | 0.84 |
| √.8 | 0.89 |
| √.9 | 0.95 |
| √.10 | 0.32 |
घनमूल
किसी संख्या का घनमूल वह संख्या हैं, जिसे परस्पर तीन बार गुणा करने पर दी गई संख्या प्राप्त होती हैं। इसे (∛) चिन्ह से दर्शाते हैं।
जैसे:- 64 का वर्गमूल = 3√64 = 4
तथा 4 × 4 × 4 = 64 अभीष्ट संख्या
घनमूल निकालने का तरीका
किसी संख्या के अभाज्य गुणनखण्डों के तीन गुणन खण्डों में से एक लेकर इनका गुणनफल ही संख्या का घनमूल होगा घनमूल वाले प्रश्न हल करने के लिए नीचे के 3 steps solve करने होते है।
- दी गई संख्या में दाई और से तीन अंको का जोड़ा बनाये और शेष अंको का जोड़ा बनाएं।
- दी गई संख्या में इकाई अंक जिस संख्या का घन करने से प्राप्त होगा वह संख्या उत्तर में सबसे अंत में लिखे।
- शेष अंकों के जोड़े से बनी हुई संख्या जिस संख्या के घन करने से उसके सबसे नजदीक पहुँचे वह संख्या उत्तर में बाई ओर लिखे।
1 से 100 तक की संख्याओं के घनमूल
| ∛1 | 1 |
| ∛8 | 2 |
| ∛27 | 3 |
| ∛64 | 4 |
| ∛125 | 5 |
| ∛216 | 6 |
| ∛343 | 7 |
| ∛512 | 8 |
| ∛729 | 9 |
| ∛1,000 | 10 |
| ∛1,331 | 11 |
| ∛1,728 | 12 |
| ∛2,197 | 13 |
| ∛2,744 | 14 |
| ∛3,375 | 15 |
| ∛4,096 | 16 |
| ∛4,913 | 17 |
| ∛5,832 | 18 |
| ∛6,859 | 19 |
| ∛8,000 | 20 |
| ∛9,261 | 21 |
| ∛10,648 | 22 |
| ∛12,167 | 23 |
| ∛13,824 | 24 |
| ∛15,625 | 25 |
| ∛17,576 | 26 |
| ∛19,683 | 27 |
| ∛21,952 | 28 |
| ∛24,389 | 29 |
| ∛27,000 | 30 |
| ∛29,791 | 31 |
| ∛32,768 | 32 |
| ∛35,937 | 33 |
| ∛39,304 | 34 |
| ∛42,875 | 35 |
| ∛46,656 | 36 |
| ∛50,653 | 37 |
| ∛54,872 | 38 |
| ∛59,319 | 39 |
| ∛64,000 | 40 |
| ∛68,921 | 41 |
| ∛74,088 | 42 |
| ∛79,507 | 43 |
| ∛85,184 | 44 |
| ∛91,125 | 45 |
| ∛97,336 | 46 |
| ∛103,823 | 47 |
| ∛110,592 | 48 |
| ∛117,649 | 49 |
| ∛125,000 | 50 |
| ∛132,651 | 51 |
| ∛140,608 | 52 |
| ∛148,877 | 53 |
| ∛157,464 | 54 |
| ∛166,375 | 55 |
| ∛175,616 | 56 |
| ∛185,193 | 57 |
| ∛195,112 | 58 |
| ∛205,379 | 59 |
| ∛216,000 | 60 |
| ∛226,981 | 61 |
| ∛238,328 | 62 |
| ∛250,047 | 63 |
| ∛262,144 | 64 |
| ∛274,625 | 65 |
| ∛287,496 | 66 |
| ∛300,763 | 67 |
| ∛314,432 | 68 |
| ∛328,509 | 69 |
| ∛343,000 | 70 |
| ∛357,911 | 71 |
| ∛373,248 | 72 |
| ∛389,017 | 73 |
| ∛405,224 | 74 |
| ∛421,875 | 75 |
| ∛438,976 | 76 |
| ∛456,533 | 77 |
| ∛474,552 | 78 |
| ∛493,039 | 79 |
| ∛512,000 | 80 |
| ∛531,441 | 81 |
| ∛551,368 | 82 |
| ∛571,787 | 83 |
| ∛592,704 | 84 |
| ∛614,125 | 85 |
| ∛636,056 | 86 |
| ∛658,503 | 87 |
| ∛681,472 | 88 |
| ∛704,969 | 89 |
| ∛729,000 | 90 |
| ∛753,571 | 91 |
| ∛778,688 | 92 |
| ∛804,357 | 93 |
| ∛830,584 | 94 |
| ∛857,375 | 95 |
| ∛884,736 | 96 |
| ∛912,673 | 97 |
| ∛941,192 | 98 |
| ∛970,299 | 99 |
| ∛1,000,000 | 100 |
वर्गमूल एवं घनमूल से संबंधित सवाल
Q.1 √5808/48 = ?
A. 11
B. 13
C. 17
D. 19
हल:- प्रश्ननानुसार,
√5808/48 = ?
√121 = ?
? = 11
Ans. 11
Q.2 √324/1.5 = ?/√256
A. 122
B. 192
C. 288
D. 432
हल:- प्रश्ननानुसार,
√324/1.5 = ?/√256
18/1.5 = ?/16
1.5 × ? = 18 × 16
? = (18 × 16)/1.5
? = (18 × 16 × 10)/15
? = 192
Ans. 192
Q.3 √196/7 × √900/? = 4
A. 15
B. 150
C. 1575
D. 5705
हल:- प्रश्ननानुसार,
√196/7 × √900/? = 4
14/7 × 30/? = 4
2 × 30/? = 4
? = (30 × 2)/4
? = 15
Ans. 15
Q.4 (√24 + √216)/√96
A. 2√6
B. 6√2
C. 2/56
D. 2
हल:- प्रश्ननानुसार,
(√24 + √216)/√96
√24(1 + √9)/√24 × √4
(1 + 3)/2
4/2
2
Ans. 2
Q.5 (√5 – √3)/(√5 – √3) का मान होगा?
A. 4 + √15
B. 4 – √15
C. 1/2
D. 1
हल:- प्रश्ननानुसार,
(√5 – √3)/(√5 – √3)
(√5 – √3) × (√5 – √3)/(√5 + √3)(√5 – √3)
[(√5)^2 + (√3)^2 – 2√5.√3]/(√5)^2 – (√3)^2
(5 + 3 – 2√15)/5 – 3
4 – √15
Ans. 6 – √15
Q.6 (√10 × √15) का मान ज्ञात कीजिए?
A. 5√6
B. √30
C. 3√15
D. √25
हल:- प्रश्ननानुसार,
(√10 × √15)
√150
5√6
Ans. 5√6
Q.7 112/√196 × √576/12 × √256/8 का मान होगा?
A. 8
B. 12
C. 16
D. 32
हल:- प्रश्ननानुसार,
(112/√196) × (√576/12) × (√256/8)
(112/14) × (24/12) × (16/8)
8 × 2 × 2
32
Ans. 32
Q.8 √(3.6 – 0.36) = ?
A. 1.8
B. 3.24
C. 10.5
D. 20.8
हल:- प्रश्ननानुसार,
√(3.6 – 0.36) = ?
√3.24 = ?
1.8 = ?
Ans. 1.8
Q.9 (√65025)² = (?)²
A. 255
B. 325
C. 510
D. 710
हल:- प्रश्ननानुसार,
(√65025)² = (?)²
(?)² = 65025
? = √65025
? = 255
Ans. 255
Q.10 √? + 7 = √576
A. 169
B. 196
C. 225
D. 289
हल:- प्रश्ननानुसार,
√? + 7 = √576
√? = √576 – 7
√? = 24 – 7
√? = 17
दोनों पक्षों का वर्ग करने पर
(√?)² = (17)²
? = 289
Ans. 289
Q.11 √?/196 = 72/56 होगा
A. 14
B. 18
C. 212
D. 324
हल:- प्रश्ननानुसार,
√?/196 = 72/56
√?/14 = 72/56
√? = (72 × 14)/56
√? = 18
दोनों पक्षों का वर्ग करने पर
(?)² = (18)²
? = 324
Ans. 324
Q.12 (√32 + √48)/(√8 + √12)
A. √2
B. 2
C. 4
D. 8
हल:- प्रश्ननानुसार,
(√32 + √48)/(√8 + √12)
(4√2 + 4√3)/2√2 + 2√3
4(√2 + √3)/2(√2 + √3)
4/2
2
Ans. 2
Q.13 √5 + 2√6 – 1/√5 + 2√6 का मान होगा?
A. 2√2
B. 2√3
C. 1 + √5
D. √5 – 1
हल:- प्रश्ननानुसार,
√5 + 2√6 – 1/√5 + 2√6
(√5 + 2√6 – 1)/√5 + 2√6
(4 + 2√6)/(√5 + 2√6)
माना, x = (4 + 2√6)/(√5 + 2√6)
दोनों तरफ वर्ग करने पर,
x^2 = (16 + 24 + 16√6)/(5 + 2√6)
x^2 = 8(5 + 2√6)/(5 + 2√6)
x^2 = 8
x = 2√2
Ans. 2√2
Q.14 √(0.02 + √.0049) बराबर हैं?
A. 0.03
B. √.72
C. 0.3
D. √0.27
हल:- प्रश्ननानुसार,
√(0.02 + √.0049)
√(0.02 + 0.07)
√0.09
0.3
Ans. 0.3
Q.15 √(15612 + √154 + √225) का मान होगा?
A. 13
B. 15
C. 25
D. 125
हल:- प्रश्ननानुसार,
√(15612 + √154 + √225)
√(15612 + √154 + 15)
√(15612 + √169)
√(15612 + 13)
√15625
125
Ans. 125
Q.16 √4/3 – √3/4 का मान होगा?
A. 1/2√3
B. -1/2√3
C. 1
D. 5√3/6
हल:- प्रश्ननानुसार,
√4/3 – √3/4
2/√3 – √3/2
(4 – 3)/2√3
1/2√3
Ans. 1/2√3
Q.17 √16 ∛512 × 8 का मान क्या हैं?
A. 8
B. 16
C. 32
D. 64
हल:- प्रश्ननानुसार,
√16 ∛512 × 8
√16∛8 × 8 × 8 × 2 × 2 × 2
√16 × 8 × 2
√16 × 16
16
Ans. 16
Q.18 √32.4/x = 0.18, तो x का मान होगा?
A. 10
B. 100
C. 200
D. 1000
हल:- प्रश्ननानुसार,
√32.4/x = 0.18
दोनों पक्षों का वर्ग करने पर
(√32.4/x)² = (0.18)²
32.4/x = 0.0324
x × 0.0324 = 32.4
x = (324 × 1000)/324
x = 1000
Ans. 1000
Q.19 √12+√12+√2+ ……..= ∞
A. 0
B. 1
C. 2
D. 4
हल:- प्रश्ननानुसार,
√12+√12+√2+ ……..= ∞
माना,
x = √12+√12+√2+ ……..= ∞
दोनों पक्षों का वर्ग करने पर
x² = (√12+√12+√2+ ……..= ∞)²
x² = 12 + x
x² – x – 12 = 0
x² – 4x + 3x – 12 = 0
x(x – 4) + 3(x – 4) = 0
(x – 4)(x + 3) = 0
x – 4 = 0, x + 3 = 0
x = 4, x = -3
x = 4
Ans. 4
Q.20 √3√3√3√3 = ?
A. 3
B. 9
C. 12
D. 18
हल:- प्रश्ननानुसार,
√3√3√3√3 = ?
माना,
x = √3√3√3√3
दोनों पक्षों का वर्ग करने पर
x² = (√3√3√3√3)²
x² = 3x
x = 3
Ans. 3
Q.21 √2 तथा √3 के मध्य एक परिमेय संख्या हैं?
A. 1.5
B. 2.5
C. 3.7
D. 8.9
हल:- प्रश्ननानुसार,
√2 और √3 के बीच ऐसी संख्या जो पूर्ण वर्ग हो = 2.25
अतः अभीष्ट परिमेय संख्या = √2.25
1.5
Ans. 1.5
Q.22 वह छोटी से छोटी पूर्ण वर्ग संख्या जो 15, 24 तथा 25 से विभक्त हैं होगी?
A. 900
B. 2025
C. 3600
D. 9000
हल:- प्रश्ननानुसार,
15,24 तथा 25 का ल.स. = 600
अतः अभीष्ट वर्ग संख्या = 600 × 6
3600
Ans. 3600
Q.23 वह छोटी से छोटी संख्या जो पूर्ण वर्ग हो तथा 3, 4, 5, 6, 8 प्रत्येक से पूर्णतया विभक्त हो क्या होगी?
A. 900
B. 1200
C. 2500
D. 3600
हल:- 3, 4, 5, 6, 8 का ल. स. = 120
120 = 2 × 2 × 2 × 3 × 5
अर्थात पूर्ण वर्ग होने के लिए उसे 2 × 3 × 5 से गुणा करना होगा।
अतः अभीष्ट संख्या = 120 × 30
= 3600
Ans. 3600
Q.24 60 का सबसे छोटा गुणज जो कि पूर्ण वर्ग हो, होगा?
A. 360
B. 600
C. 900
D. 3600
हल:- प्रश्ननानुसार,
60 = 2 × 2 × 3 × 5
अर्थात पूर्ण वर्ग होने के लिए उसे 3 × 5 से गुणा करना होगा।
अतः अभीष्ट संख्या = 60 × 3 × 5
= 900
Ans. 900
Q.25 (/21) × (/189) में प्रत्येक * के स्थान पर कौन सी संख्या आएगी?
A. 3969
B. 147
C. 39
D. 63
हल:- माना * के स्थान पर x हैं, तो x²/(21 × 189) = 1
x = √189 × 21
x = √7 × 3 × 7 × 27
x = 7 × 9
x = 63
Ans. 63
Q.26 दो संख्याओं का योग 100 व अंतर 37 हैं उनके वर्गों में अंतर होगा?
A. 37
B. 100
C. 3700
D. 1037
हल:- माना कि एक संख्या = a
तथा दूसरी संख्या = b
प्रश्ननानुसार,
a + b = 100
a – b = 37
a² – b² = (a + b)(a – b)
a² – b² = 100 × 37
a² – b² = 3700
Ans. 3700
Q.27 यदि 23 = √13 तथा 34 = 5 हो, तो 5*12 का मान होगा?
A. 12
B. 13
C. √17
D. √29
हल:- 5*12
= √(5² + 12²)
= √25 + 144
= √169
= 13
Ans. 13
Q.28 दिया हैं कि √10 = 3.16 हैं, तो √0.9 का निकटतम मान क्या हैं?
A. 0.9493
B. 0.8808
C. 98.780
D. 0.5620
हल:- √0.9
√9/10
3/3.16
0.9493
Ans. 0.9493
Q.29 यदि √3 = 1.732 हो, तो 1/√3 किसके बराबर होगा?
A. 0.057
B. 5.770
C. 0.755
D. 0.577
हल:- प्रश्ननानुसार,
1/√3
= √3/3
= 1.732/3
= 0.577
Ans. 0.577
Q.30 यदि √5 = 2.2360 दिया हैं, तो √180 – √80 बराबर होगा?
A. 4.4720
B. 5
C. 7
D. 48.90
हल:- प्रश्ननानुसार,
√180 – √180
6√5 – 4√5
2√5
2 × 2.2360
4.4720
Ans. 4.4720
Q.31 यदि √24 = 4.899 तो √8/3 का मान होगा?
A. 0.544
B. 1.333
C. 1.633
D. 2.666
हल:- प्रश्ननानुसार,
√8/3 = √8/3 × √3/3
√24/3
4.899/3
1.633
Ans. 1.633
Q.32 यदि a = 4 और b = 6 हो तो, a/4√(4b² – a²) का मान होगा?
A. 12
B. √128
C. √35
D. 4√18
हल:- प्रश्ननानुसार,
4/4√4 × 36 – 16
√144 – 16
√128
Ans. √128
Q.33 व्यंजक 11.98 × 11.98 + 11.98 × x + 0.02 × 0.02 पूर्ण वर्ग होगा यदि x बराबर ? हो, तो ? का मान होगा?
A. 0.02
B. 0.2
C. 0.04
D. 0.4
हल:- माना,
a = 11.98 और b = 0.02
व्यंजक = a² + a × x + b²
व्यंजक को पूर्ण होने के लिए,
x = 2b
x = 2 × 0.02
x = 0.04
Ans. 0.04
Q.34 यदि √a + √b = 17 तथा √a – √b = 1 हो तो √ab का मान हैं?
A. 17
B. 18
C. 72
D. 86
हल:- प्रश्ननानुसार,
√a + √b = 17……(1)
√a – √b = 1………(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर
2√a = 18
√a = 9 और √b = 8
√a.√b = 9 × 8
√a.√b = 72
√ab = 72
Ans. 72
Q.35 यदि √289 ÷ √x = 1/5, तो x का मान होगा?
A. 17/25
B. 8796
C. 29/47
D. 7225
हल:- प्रश्ननानुसार,
√289 ÷ √x = 1/5
17/√x = 1/5
√x = 17 × 5
दोनों पक्षों का वर्ग करने पर
(√x)² = (85)²
x = 7225
Ans. 7225
Q.36 यदि x * y = √(x + y)(y² – 12x)/(x – 2)(y – 7), तो 5 * 9 का मान होगा?
A. 4
B. 7
C. 9
D. 11
हल:- प्रश्नानुसार,
5 * 9 = √(5 + 9)(9² – 12 × 5) / (5 – 2)(9 – 7)
5 * 9 = √(14 × 21)/(3 × 2)
5 * 9 = √(7 × 7)
5 * 9 = 7
Ans. 7
Q.37 यदि 2 * 3 = √13 तथा 3 × 4 = 5 हो, तो 5 * 12 का मान होगा?
A. √17
B. √29
C. 12
D. 13
हल:- प्रश्नानुसार,
5 * 12 = √5² + 12²
5 * 12 = √25 + 144
5 * 12 = √169
5 * 12 = 13
Ans. 13
Q.38 यदि √2 = 1.4142 हो, तो ½ (√2 – 1/√2 + 1) का मान होगा?
A. 0.085
B. 0.086
C. 0.850
D. 0.860
हल:- प्रश्नानुसार,
½ [(√2 – 1)/(√2 + 1)] = ½ (√2 – 1)(√2 – 1)/(√2 + 1)(√2 – 1)
= ½ × (2 + 1 – 2√2)/2 – 1
= ½ × (3 – 2√2)
= ½ (3 – 2 × 1.4142)
= ½ (3 – 2.8284)
= ½ × 0.1716
= 0.0858
= 0.086
Ans. 0.086
Q.39 (*/21) × (*/189) = 1 में प्रत्येक * के स्थान पर कौन सी संख्या आएगी?
A. 3969
B. 147
C. 63
D. 21
हल:- प्रश्नानुसार,
माना * के स्थान पर x हैं, तो
x² /21 × 89 = 1
x² = 21 × 89
x = √21 × 89
x = √7 × 3 × 7 × 27
x = 7 × 9
x = 63
Ans. 63
Q.40 दो संख्याओं का योग 100 व अंतर 37 हैं उनके वर्गों में अंतर होगा?
A. 37
B. 63
C. 100
D. 3700
हल:- माना कि एक संख्या = a
तथा दूसरी संख्या = b
प्रश्नानुसार,
a + b = 100 तथा
a – b = 37
a² – b² = (a + b) (a – b)
= 37 × 100
= 3700
Ans. 3700
| जरूर पढ़े : | ||
| त्रिकोणमिति | क्षेत्रमिति | समय दूरी और चाल |
| समय और कार्य | बीजगणित सर्वसमिका | गणित के महत्वपूर्ण सूत्र |
आशा है वर्गमूल एवं घनमूल की यह जानकारी आपको पसंद आएगी और आप इसको पढ़कर आसानी से वर्गमूल एवं घनमूल के प्रश्नो को हल कर पाएंगे।
वर्गमूल एवं घनमूल से संबंधित किसी भी प्रश्न के लिए कमेंट करे और यदि जानकारी पसंद आयी है तो पोस्ट को Social sites पर शेयर जरूर करे।


My name is roshan raj please question send me
Hello Roshan,
Ap question ko post me read kar skte hai.