इस पेज पर आप गणित के महत्वपूर्ण अध्याय बीजगणित सर्वसमिकाएँ एवं उनसे संबंधित ट्रिक्स और उदाहरण को पढ़ेंगे। क्योकि इस टॉपिक से एक-दो प्रश्न परीक्षा में पूछ ही लिए जाते हैं।
पिछले पेज पर हमने गणित के महत्वपूर्ण अध्याय अनुपात और समानुपात की जानकारी शेयर कर चुके है उसे जरूर पढ़े।
चलिए अब बीजगणतीय के अध्याय को पढ़कर समझते है।
बीजगणित
बीजगणित संख्या पद्वति, ज्यामिति, विश्लेषण के साथ गणित के व्यापक भागों में से एक हैं
बीजगणित, गणित की वह शाखा हैं जिसमें संख्याओ के स्थान पर चिन्हों का प्रयोग किया जाता हैं बीजगणित चर तथा अचर राशियों के समीकरण को हल करने तथा चर राशियों के मान निकालने पर आधारित हैं
बीजगणित के विकास के फलस्वरूप निर्देशांक ज्यामिति व कैलकुलस का विकास हुआ जिससे गणित की उपयोगिता तीव्र गति से बढ़ गई बीजगणित से विज्ञान और तकनीकी के विकास को गति मिली।
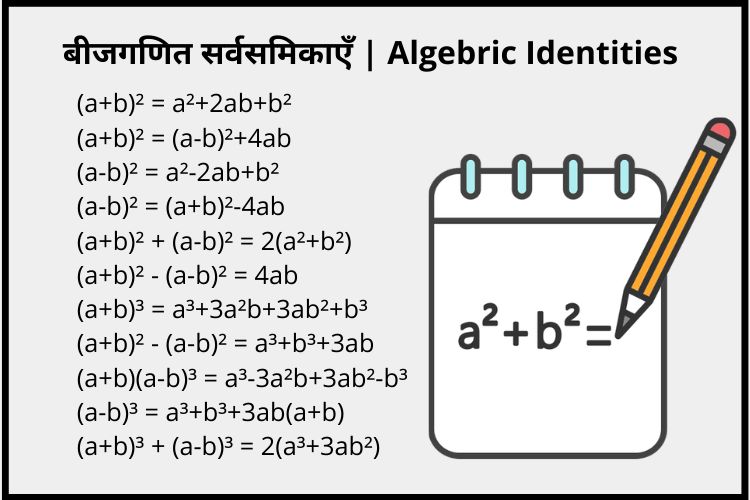
बीजगणितीय सर्वसमिकाएँ
- (a+b)² = a²+2ab+b²
- (a+b)² = (a-b)²+4ab
- (a-b)² = a²-2ab+b²
- (a-b)² = (a+b)²-4ab
- (a+b)² + (a-b)² = 2(a²+b²)
- (a+b)² – (a-b)² = 4ab(a+b)³ = a³+3a²b+3ab²+b³
- (a+b)² – (a-b)² = a³+b³+3ab(a+b)
- (a-b)³ = a³-3a²b+3ab²-b³
- (a-b)³ = a³+b³+3ab(a+b)
- (a+b)³ + (a-b)³ = 2(a³+3ab²)
- (a+b)³ + (a-b)³ = 2a(a²+3b²)
- (a+b)³ – (a-b)³ = 3a²b+2b³
- (a+b)³ – (a-b)³ = 2b(3a²+b²)
- a²-b² = (a-b)(a+b)
- a³+b³ = (a+b)(a²-ab+b²)
- a³-b³ = (a-b)(a²+ab+b²)
- a³-b³ = (a-b)³ + 3ab(a-b)
- (a+b+c)² = a²+b²+c²+2(ab+bc+ca)
- (a+b+c)³ = a³+b³+c³+3(a+b)(b+c)(c+a)
- a³+b³+c³ = (a+b+c)³ – 3(a+b)(b+c)(c+a)
- (a+b+c+d)² = a²+b²+c²+d²+2(ab+ac+ad+bc+bd+cd)
- a³+b³+c³-3abc = (a+b+c)(a²+b²+c²-ab-bc-ca)
- x²+y²+z²-xy-yz-zx = ½[(x-y)²+(y-z)²+(z+x)²]
- a³+b³+c³-3abc = ½(a+b+c) [(a-b)²+(b-c)²+(c-a)²]
- a²+b²+c²-ab-bc-ca = ½[(a-b)²+(b-c)²+(c-a)²]
- a(b-c)+b(c-a)+c(a-b)=0
- ab(a-b)+bc(b-c)+ca(c-a) = -(a-b)(b-c)(c-a)
- a²(b²-c²)-b²(c²-a²)+c²(a²-b²) = (a-b)(b-c)(c-a)
- a+b = (a³+b³)/(a²+ab+b²)
- a – b = (a³-b³)/(a²+ab+b²)
- a+b+c = (a³+b³+c³-3abc)/(a²+b²+c²-ab-bc-ca)
- (a+1/a)² = a²+1/a²+2
- (a²+1/a²) = (a+1/a)²-2
- (a-1/a)² = a²+1/a²-2
- (a²+1/a²) = (a-1/a)²+2
- (a³+1/a³ = (a+1/a)³-3(a+1/a)
- (a³-1/a³ = (a-1/a)³-3(a-1/a)
जरूर पढ़िए :
बीजगणित के उदाहरण
Q.1 यदि x + y = 8 हो तो x, y का अधिकतम मान क्या होगा?
A. 8
B. 16
C. 24
D. 32
हल:- x + y = 8
x = 4, y = 4
4 + 4 = 8
x = y = 4
x, y का max^m = 4 × 4
Ans. 16
Q.2 (x – 2)(x – 9) का न्यूनतम मान क्या होगा?
A. -11/4
B. 49/4
C. 0
D. -49/4
हल:- (x – 2)(x – 9)
x² – 11x + 18
a = 1, b = -11, c = 18
Trick:
c – (b²/4a)
18 – (-11²/4×1)
18 – 121/4
(72 – 121)/4
Ans. -49/4
Q.3 (-4 x² + 12x – 2) का अधिकतम मान होगा?
A. 2/3
B. 3/2
C. 7
D. 0
हल:- -4x² + 12x – 2
a = -4, b =12, c = -2
Trick:
c – (b²/4a)
-2 – (12²/4×-4)
-2 – (144/-16)
-2 + 144/16
(-32 + 144)/16
112/16
Ans. 7
Q.4 यदि (x + 1/x)³ = 3 हो, तो x³ + 1/x³ किसके बराबर होगा?
A. 3
B. 2
C. 1
D. 0
हल:- (x + 1/x)² = 3
(x + 1/x) = √3 —————(1)
(x + 1/x)³ = (√3)³
(a+b)³ = a³+3a²b+3ab²+b³
(a+b)³ = a³+b³+3ab(a+b)
(x + 1/x) = x³ + 1/x³ – 3x*1/x(x + 1/x)
(x + 1/x) = x³ + 1/x³ – 3(x + 1/x)
(x + 1/x) = (x+1/x)³ – 3(x + 1/x)
समीकरण (1) से,
(√3)³ – 3√3
3√3 – 3√3
Ans. 0
Q.5 2x + 2/x = 1 हो, तो x³+1/x³ का मान होगा?
A. 13/8
B. -11/8
C. 11/8
D. -13/8
हल:- 2x + 2/x = 1
2 (x + 1/x) = 1
x + 1/x = 1/2
दोनों पक्षों का घन करने पर
(x + 1/x)³ = (1/2)³
x³ + 1/x³ – 3x*1/x (x + 1/x) = 1/8
(x + 1/x)³ – 3(x + 1/x) = 1/8
(1/2)³ – 3*1/2 = 1/8
1/8 – 3/2 = 1/8
(1 – 12)/8 = 1/8
-11/8 = 1/8
x³ + 1/x³ = -11/8
Ans. -11/8
Q.6 यदि 2x + 1/3x = 16 हो, तो 3x + 1/2x = ?
A. 4
B. 8
C. 9
D. 12
हल:- 2x + 1/3x = 6
दोनों तरफ 3/2 से गुणा करने पर
3/2(2x + 1/3x) = 6 * 3/2
3/2(6x + 1)/3x = 3 * 3
(18x² + 3)/6x = 9
18x²/6x + 3/6x = 9
3x + 1/2x = 9
Ans. 9
Q.7 यदि x + 1/x = 5 हो, तो 2x / 3x^2 – 5x + 3 किस के बराबर होगा?
A. 1/2
B. 1/3
C. 1/4
D. 1/5
हल:- x + 1/x = 5
2x / (3x² – 5x + 3)
अंश एवं हर में x से भाग देने पर
2x/x / (3x² – 5x + 3)/x
2 / (3x²/x – 5x/x + 3/x)
2 / (3x – 5 + 3/x)
2 / (3x + 3/x – 5)
2 / 3(x + 1/x) – 5
2 / 3 * 5 – 5
2 / 15 – 5
2 / 10
Ans. 1 / 5
Q.8 यदि x ≥ 1 और x² + 1/x² = 83 हो, तो x³ – 1/x³ कितना होगा?
A. 756
B. 760
C. 764
D. 750
हल;- x² + 1/x² = 83
दोनों तरफ 2 घटाने पर
x² + 1/x² – 2 = 83 – 2
(x² + 1/x)² = 81
x – 1/x = 9
x³ – 1/x³ = (1 – 1/x)³ + 3x*1/x(x – 1/x)
(9)³ + 39
729 + 27
Ans. 756
Q.9 यदि a² – 4a – 1 = 0 हो, तो a² + 1/a² + 3a – 3/a का मान हैं?
A. 25
B. 30
C. 35
D. 40
हल: प्रश्नानुसार
a² – 4a – 1 = 0
a² – 1 = 4a
दोनों पक्षों में a से भाग देने पर
a²/a – 1/a = 4a/a
a – 1/a = 4 ……..(1)
दिया हैं,
a² + 1/a² + 3a – 3/a
(a – 1/a)² + 3(a – 1/a)
समीकरण (1) से,
(4)² + 2 + 3 × 4
16 + 2 + 12
Ans. 30
Q.10 यदि x² – 3x + 1 = 0 हो, तो x² + x + 1/x + 1/x² का मान हैं?
A. 10
B. 2
C. 6
D. 8
हल: प्रश्नानुसार
x² – 3x + 1 = 0
x² + 1 = 3x
दोनों पक्षों में x से भाग देने पर
x²/x + 1/x = 3x/x
x + 1/x = 3 ……..(1)
दिया हैं,
x² + x + 1/x + 1/x²
x² + 1/x² + (x + 1/x)
(x + 1/x)² – 2 x*1/x + (x + 1/x)
समीकरण (1) से,
(3)² – 2 + 3
9 – 2 + 3
12 – 2
Ans. 10
बीजगणित से संबंधित प्रश्न और हल
Q.11 यदि 3x – 1/4y = 6 हो, तो 4x – 1/3y का मान होगा?
A. 2
B. 4
C. 6
D. 8
हल: प्रश्नानुसार,
3x – 1/4y = 6
दोनों पक्षों में 4/3 से गुणा करने पर
4/3(3x – 1/4y) = 64/3
4/33x – 1/4y * 4/3 = 4*2
4x – 1/3y = 8
Ans. 8
Q.12 यदि a + b + c = 0 हो, तो (a² + b² + c²) / (a² – bc) ) का मान क्या होगा?
A. 0
B. 1
C. 2
D. 3
हल: प्रश्नानुसार,
a + b + c = 0
a = (-b – c)
दोनों पक्षों का वर्ग करने पर
a² = (-b – c)²
a² = b² + c² + 2bc
दिया हैं,
(a² + b² + c²) / (a² – bc)
समीकरण (1) से,
(b² + c² + 2bc + b² + c²) / (b² + c² + 2bc – bc)
(2b² + 2c² + 2bc) / (b² + c² + bc)
2(b² + c² + bc) / (b² + c² + bc)
Ans. 2
Q.13 यदि a + b + 1 = 0 हो, तो ( a³ + b³ + 1 – 3ab) का मान क्या होगा?
A. 0
B. 2
C. 4
D. 5
हल: प्रश्नानुसार,
a + b + 1 = 0
a + b = -1
दोनों पक्षों का घन करने पर
(a + b)³ = (-1)³
a³ + b³ + 3ab(a + b) = -1
a³ + b³ + 1 – 3ab = 0
Ans. 0
Q.14 a + b + c = 0 हो, तो a³ + b³ + c³ किसके बराबर होगा?
A. 2abc
B. 3abc
C. a + b + c
D. abc
हल: प्रश्नानुसार,
a + b + c = 0
(a + b + c)³ = 0
a³ + b³ + c³ – 3abc
(a + b + c) (a² + b² + c² – ab – bc – ca)
0 * (a² + b² + c² – ab – bc – ca)
0
a³ + b³ + c³ – 3abc = 0
a³ + b³ + c³ – 3abc = 0
0 – 3abc = 0
Ans. 3abc
Q.15 यदि a + b + c = 2s हो, तो (s – a)² + (s – b)² + (s – c)² + s² – a² – b² – c² = ?
A. -1
B. 1
C. 0
D. 2
हल: प्रश्नानुसार,
a + b + c = 0
2s = a + b + c ………..(1)
दिया हैं,
(s – a)² + (s – b)² + (s – c)² + s² – a² – b² – c²
s² + a² – 2sa + s² + b² – 2sb + s² + c² – 2sc + s² – a² – b² – c²
s² + s² + s² + s² – 2sa – 2sb – 2sc + a² + b² + c² – a² – b² – c²
4s² – 2s(a + b + c)
समीकरण (1) से,
4s² – 2s(2s)
4s² – 4s²
Ans. 0
Q.16 यदि a = 225, b = 226, c = 227 हो, तो a³ + b³ + c³ – 3abc का मान क्या होगा?
A. 2304
B. 2430
C. 2034
D. 2340
हल: प्रश्नानुसार,
a = 225,
b = 226,
c = 227
a³ + b³ + c³ – 3abc = ½(a + b + c)
[(a – b)² + (b – c)² + (c – a)²]
½(225 + 226 + 227)
½ × 678(1² + 1² + 2²)
½ × 678(1 + 1 + 4)
½ × 678 × 6
678 × 3
Ans. 2034
Q.17 यदि x + 1/16x = 1 हो, तो 64 x^3 + 1/64 x^3 का मान होगा?
A. 4
B. 52
C. 64
D. 76
हल: प्रश्नानुसार,
x + 1/16x = 1
दोनों तरफ 4 से गुणा करने पर,
4x + 4/16x = 1 × 4
4x + 1/4x = 4 ………(1)
दोनों तरफ घन करने पर
(4x + 1/4x)³ = (4)³
[(a +b)³ = a³ + b³ + 3(a + b)]
(4x)³ + (1/4x)³ + 3(4x + 1/4x) = 64
64x³ + 1/64x³ + 3(4x + 1/4x) = 64
समीकरण (1) से,
64x³ + 1/64x³ + 3 × 4 = 64
64x³ + 1/64x³ + 12 = 64
64x³ + 1/64x³ = 64 – 12
64x³ + 1/64x³ = 52
Ans. 52
Q.18 यदि P + Q = 10 और PQ = 5 हो, तो P/Q + Q/P का संख्यात्मक मान होगा?
A. 16
B. 18
C. 20
D. 22
हल: प्रश्नानुसार,
P + Q = 10
दोनों पक्षों का वर्ग करने पर
(P + Q)² = (10)²
P² + Q² + 2PQ = 100
दिया हैं,
PQ = 5
P² + Q² + 2 × 5 = 100
P² + Q² + 10 = 100
P² + Q² = 100 – 10
P² + Q² = 90
प्रश्नानुसार,
P/Q + Q/P
(P² + Q²)/PQ
90/5
Ans. 18
Q.19 यदि a² + 1/a² = 98 हो, तो a³ + 1/a³ का मान होगा?
A. 535
B. 790
C. 970
D. 1030
हल: प्रश्नानुसार,
a² + 1/a² = 98
(a² + 1/a² + 2) = 98 + 2
(a +1/a)² = 100
(a + 1/a)² = (10)²
a + 1/a = 10
दोनों पक्षों का घन करने पर
(a + 1/a)³ = (10)³
a³ + 1/a³ – 3(a + 1/a) = 1000
a³ + 1/a³ – 3 × 10 = 1000
a³ + 1/a³ – 30 = 1000
a³ + 1/a³ = 1000 – 30
a³ + 1/a³ = 970
Ans. 970
Q.20 x + 4/x = 4 हो, तो x³ + 4/x³ का मान कितना होगा?
A. 8
B. 17/2
C. 16
D. 23/2
हल: प्रश्नानुसार,
x + 4/x = 4
(x² + 4)/x = 4
x² + 4 = 4x
x² – 4x + 4 = 0
(x – 2)² = 0
x – 2 = 0
x = 2
दिया हैं,
x³ + 4/x³
x का मान रखने पर,
(2)³ + 4/(2)³
8 + 4/8
8 + 1/2
Ans. 17/2
जरूर पढ़िए :
इस पेज पर आपने गणित के अध्याय बीजगणितीय सर्वसमिकाएँ के बारे में पड़ा और ज्यामिति से संबंधित कुछ प्रश्नों को डायग्राम के द्वारा समझा है।
उम्मीद है कि आपको यह टॉपिक अच्छे से समझ आया होगा। यदि आपके मन में इस टॉपिक को लेकर अभी भी कोई प्रश्न हैं तो कमेंट में पूछे।