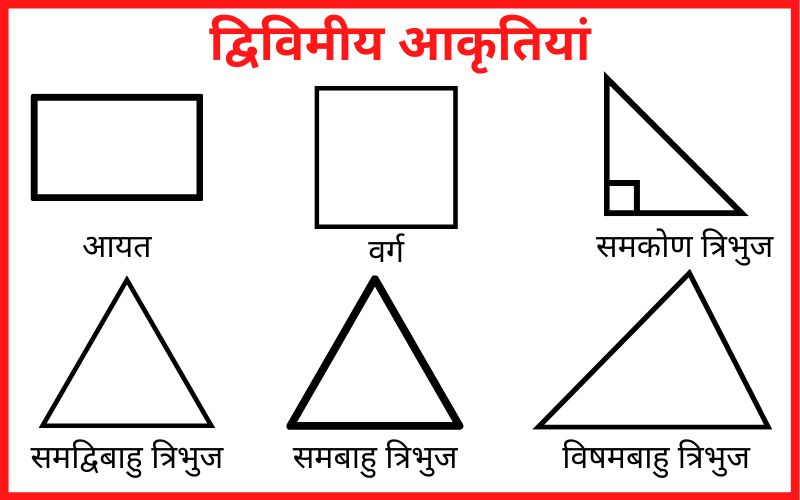
द्विविमीय आकृति की परिभाषा, सूत्र और उदाहरण

इस पेज पर हम क्षेत्रमिति के अंतर्गत द्विविमीय आकृति के बारे में पड़ेगें।

पिछले पेज पर हमने गणित विषय के अध्याय क्षेत्रमिति को शेयर किया हैं तो उसे जरूर पढ़े।

चलिए इस पेज पर द्विविमीय आकृति के बारे में पढ़ते और समझते हैं।

द्विविमीय आकृतियां किसे कहते हैं

ज्यामिति में द्वी-आयामी आकृति एक समतल आकृति होती हैं जिसमें लम्बाई और चौड़ाई के दो आयाम होते हैं। द्वी-आयामी को 2D आकृति भी कहाँ जा सकता हैं।

2D आकृति की क्षेत्रफल और परिमाप की गणना की जा सकती हैं। 2D आकृतियों में मोटाई नहीं होती हैं इसे दो तरफ से मापा जा सकता हैं।

द्विविमीय आकृतियों के अंर्तगत आयत, वर्ग, त्रिभुज आदि आते हैं।

1. आयत

चार भुजाओं से घिरी आकृति जिसमें आमने सामने की भुजाएँ समान्तर और बराबर होती हैं तथा प्रत्येक कोण समकोण होता है आयत कहलाता हैं।

AC तथा BD को विकर्ण कहते हैं तथा ये विकर्ण आपस में बराबर होते हैं अर्थात AC = BD

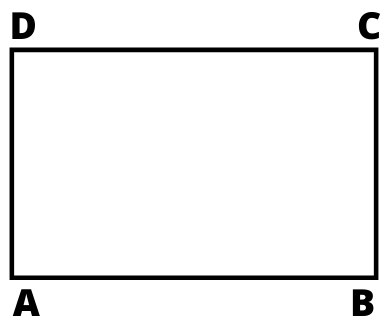
आयत का परिमाप = 2(लम्बाई + चौड़ाई)
आयत का क्षेत्रफल = लंबाई ×चौड़ाई
आयत का विकर्ण =√(लंबाई² + चौड़ाई²)

2. वर्ग

चार भुजाओं से घिरी वह आकृति जिसकी चारों भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण हो अर्थात 90° का हो, उसे वर्ग कहते हैं।

AC तथा BD को विकर्ण कहते हैं तथा विकर्ण आपस में एक दूसरे के बराबर होते हैं अर्थात AC = BD

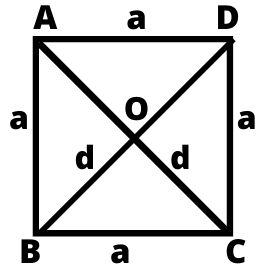
वर्ग का क्षेत्रफल = (एक भुजा)² = a²
वर्ग का क्षेत्रफल = ½ × (विकर्णो का गुणनफल) = ½ × AC × BD
वर्ग की परिमिति = 4 × a
वर्ग का विकर्ण = एक भुजा × √2 = a × √2
वर्ग का विकर्ण = √2 × वर्ग का क्षेत्रफल

तीन भुजाओं से घिरा समतल क्षेत्र त्रिभुज कहलाता हैं किसी भी त्रिभुज में तीन भुजाएं, तीन शीर्ष तथा तीन कोण होते हैं त्रिभुज के तीनों कोणों का योग 180° होता हैं। त्रिभुज के लिए ‘∆’ चिन्ह का प्रयोग किया जाता हैं।

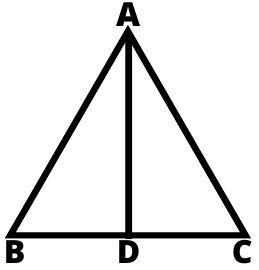
त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई

त्रिभुज के प्रकार

त्रिभुज के 6 प्रकार होते हैं।

द्विविमीय आकृतियों से संबंधित उदाहरण

प्रश्न1. एक आयताकार मैदान की लंबाई और चौड़ाई का अनुपात 5 : 3 हैं यदि मैदान का क्षेत्रफल 960 मीटर² हो तो मैदान के चारों और तीन बार लपेटने में कुल कितना तार लपेटना पड़ेगा?
A. 150 मीटर
B. 240 मीटर
C. 241 मीटर
D. 284 मीटर

हल:- आयताकार मैदान की लंबाई = 5x मीटर
तथा आयताकार मैदान की चौड़ाई = 3x मीटर
आयताकार मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
630 = (5x) × (3x)
630 = 15 x²
x² = 630/15
x² = 64
x = 8 मीटर
अतः लम्बाई = 5x
5 × 8 = 40 मीटर
तथा चौड़ाई = 3x
3 × 8 = 24 मीटर
आयताकार मैदान का परिमाप = 2 (लम्बाई + चौड़ाई)
= 2(40 + 24)
= 2 × 64
= 128 मीटर
अतः तीन चक्कर में लपेटा गया कुल तार = 3 × परिमाप
= 3 × 128
Ans. 384 मीटर

प्रश्न2. एक आयत की लम्बाई 15 सेंटीमीटर और इसके विकर्ण की लम्बाई 17 सेंटीमीटर हो तो आयत का क्षेत्रफल कितना होगा?
A. 120 वर्ग सेंटीमीटर
B. 220 वर्ग सेंटीमीटर
C. 60 वर्ग सेंटीमीटर
D. 180 वर्ग सेंटीमीटर

हल:- विकर्ण = 17 सेंटीमीटर
लम्बाई = 15 सेंटीमीटर
आयत का विकर्ण =√(l² + b²)
17 = √l² + (15)²
(17)² = l² + (15)²
(17)² – (15)² = l²
289 – 225 = l²
L² = 64
L = 8
आयत का क्षेत्रफल = l × b
= 8 × 15
Ans. 120 वर्ग सेंटीमीटर।

प्रश्न3. एक आयताकार खेत के चारों और अंदर से सीमा से लगा हुआ 8 मीटर चौड़ा रास्ता बना हैं यदि खेत को लम्बाई और चौड़ाई क्रमशः 220 मीटर और 180 मीटर हो तो रास्ता का क्षेत्रफल क्या होगा?
A. 2,014 वर्ग मीटर
B. 3,024 वर्ग मीटर
C. 4,879 वर्ग मीटर
D. 6,144 वर्ग मीटर

हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 220 × 180
= 39,600 वर्ग मीटर
लम्बाई = 220 – 16
लम्बाई = 204
चौड़ाई = 180 – 16
चौड़ाई = 164
क्षेत्रफल = लम्बाई × चौड़ाई
= 204 × 164
= 33,456 वर्ग मीटर
रास्ते का क्षेत्रफल = 39,600 – 33,456
= 6,144
Ans. 6,144 वर्ग मीटर।

प्रश्न4. एक आयत का क्षेत्रफल 252 वर्ग सेंटीमीटर हैं। इसकी लम्बाई तथा चौड़ाई 9 : 7 हैं, इसका परिमाप क्या हैं?
A. 87 सेंटीमीटर
B. 56 सेंटीमीटर
C. 87 सेंटीमीटर
D. 64 सेंटीमीटर

हल:- आयत का क्षेत्रफल = 252
लम्बाई = 9
चौड़ाई = 7
9x × 7x = 252
63x² = 252
x² = 4
x = 2
9 × 2 = 18
7 × 2 = 14
आयत का परिमाप = 2(l + b)
= 2(18 + 14)
= 2 × 32
= 64
Ans. 64 सेंटीमीटर।

प्रश्न5. उस वर्ग का क्षेत्रफल कितना होगा जिसके विकर्ण की लंबाई 8 सेंटीमीटर हैं?
A. 28 सेंटीमीटर
B. 32 सेंटीमीटर
C. 8 सेंटीमीटर
D. 18 सेंटीमीटर

हल:- क्षेत्रफल = d²/2
क्षेत्रफल = 8²/2
= (8 × 8)/2
= 8 × 4
= 32
Ans. 32 सेंटीमीटर।

प्रश्न6. एक त्रिभुज की भुजाएं क्रमशः 3 सेंटीमीटर, 4 सेंटीमीटर, और 5 सेंटीमीटर हैं इसका क्षेत्रफल क्या होगा?
A. 6 वर्ग सेंटीमीटर
B. 8 वर्ग सेंटीमीटर
C. 10 वर्ग सेंटीमीटर
D. 12 वर्ग सेंटीमीटर

हल:- प्रश्ननानुसार,
a = 3 सेंटीमीटर
b = 4 सेंटीमीटर
c = 5 सेंटीमीटर
त्रिभुज की तीनों भुजाओं का योग = (a + b + c)/2
s = (3 + 4 + 5)/2
s = 12/2
s = 6
त्रिभुज का क्षेत्रफल = √s(s – a)(s – b)(s – c)
∆ = √6(6 – 3)(6 – 4)(6 – 5)
∆ = √6 × 3 × 2 × 1
∆ = √36
∆ = 6
Ans. 6 वर्ग सेंटीमीटर।

प्रश्न7. किसी त्रिभुज PQR की भुजाएँ 5 सेमी. 12 सेमी. तथा 13 सेमी. हैं त्रिभुज में एक अन्तः वृत्त बनाया गया हैं उस वृत्त का क्षेत्रफल (वर्ग सेमी.) में हैं?
A. 4π
B. 3π/4
C. π
D. 4

हल:- माना,
वृत्त की त्रिज्या r सेमी. हैं
r = √1/15(15 – 5)(15 – 12)(15 – 13)
r = √1/15 × 10 × 3 × 2
r = √4
r = 2 सेमी.
वृत्त का क्षेत्रफल = πr²
= π2²
= 4π
Ans. 4π

उम्मीद हैं आपको द्विविमीय आकृति की जानकारी पसंद आयीं होगीं।

द्विविमीय आकृति से संबंधित किसी भी प्रश्न के लिए कमेंट करें।