शंकु की परिभाषा, सूत्र और उदाहरण

इस पेज पर हम शंकु की समस्त जानकारी को पड़ेगें तो पोस्ट को पूरा जरूर पढ़िए।

पिछले पेज पर हमने वृत्त की जानकारी शेयर की हैं तो उस आर्टिकल को जरूर पढ़े।

चलिए आज हम शंकु की जानकारी को पढ़ते और समझते हैं।

शंकु की परिभाषा

शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।

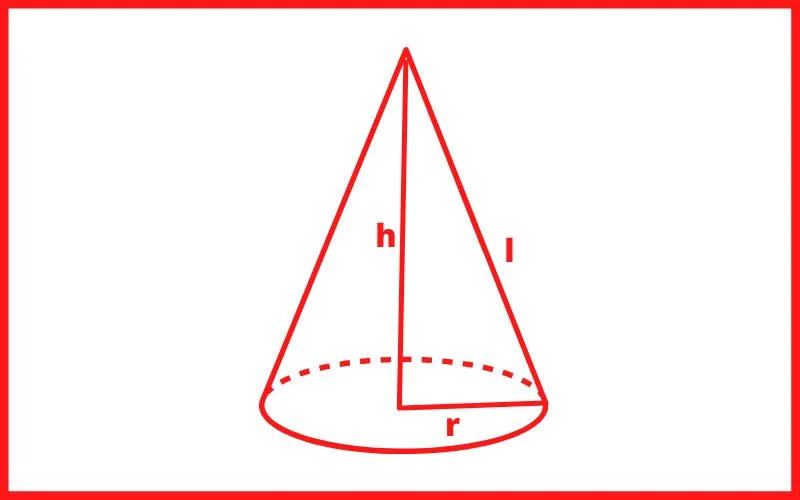
कोई समकोण त्रिभुज अपने स्थिर लम्ब के चारों ओर घूमकर जिस पिण्ड का निर्माण करता हैं उसे लम्बवृत्तीय शंकु कहते हैं।

दूसरे शब्दों में, शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।

AC या AE को तिर्यक ऊँचाई तथा CAE को शीर्ष तथा कोण BAC को अर्द्ध शीर्ष कोण कहते हैं।

माना, आधार की त्रिज्या r, ऊँचाई h तथा तिर्यक ऊँचाई हो, तो

शंकु के सूत्र

• शंकु का आयतन = ⅓ × आधार का क्षेत्रफल × ऊँचाई
  = ⅓ π²h = (πr²h)/3 घन सेंटीमीटर
• शंकु का वक्रतल = ½ × आधार की परिधि × तिर्यक ऊँचाई
  = πrl वर्ग सेंटीमीटर।
• शंकु का सम्पूर्ण सतह = वक्रप्रष्ठ + आधार का क्षेत्रफल
  = πr (l + r) वर्ग सेंटीमीटर
• शंकु की तिर्यक ऊँचाई = √(त्रिज्या)² + (ऊँचाई)²
  L = √r² + h²

शंकु के उदाहरण

Q.1 यदि किसी लम्बवृत्तीय शंकु के आधार का व्यास 14 मीटर और ऊँचाई 3 मीटर हो, तो उसका आयतन निम्नलिखित में कौन-सा होगा?
A. 154 घन मीटर
B. 154 वर्ग मीटर
C. 165 मीटर
D. 180 घन मीटर

हल:- प्रश्नानुसार,
अभीष्ट आयतन = ⅓ πr ²h
= ⅓ × ²²⁄₇ × (7)² × 3
= 154 घन मीटर
Ans. 154 घन मीटर

Q.2 यदि 24 सेंटीमीटर ऊँचाई वाले एक लम्ब वृत्तीय शंकु का आयतन 1232 सेंटीमीटर^3 हैं तो उसका वक्र पृष्ठीय क्षेत्रफल (π = ²²⁄₇) हैं?
A. 1254 सेंटीमीटर²
B. 704 सेंटीमीटर²
C. 550 सेंटीमीटर²
D. 154 सेंटीमीटर²

हल:- प्रश्नानुसार,
लम्ब वृत्तीय शंकु का आयतन = ⅓ πr²h
1232 = ⅓ × ²²⁄₇ × r² × 24
r = 7
शंकु की तिर्यक ऊँचाई = √h² + r²
= √(24)² × (7)²
= 25 सेंटीमीटर
शंकु का वक्रप्रष्ठ = πrl
= 22/7 × 7 × 25
= 550 वर्ग सेंटीमीटर
Ans. 550 वर्ग सेंटीमीटर

Q.3 शंकु की त्रिज्या 35 मीटर और शंकु की ऊँचाई 12 मीटर हैं, तो इसके वक्रप्रष्ठ का क्षेत्रफल ज्ञात कीजिए?
A. 4070 वर्ग मीटर
B. 3540 वर्ग मीटर
C. 3546 वर्ग मीटर
D. 3240 वर्ग मीटर

हल:- प्रश्नानुसार,
r = 35 मीटर
h = 12 मीटर
l = √r² + h²
l = √(35)² + (12)²
l = √1225 + 144 मीटर
l = √1369
l = 37 मीटर
वक्रप्रष्ठ का क्षेत्रफल = πrl
= 22/7 × 35 × 37 वर्ग मीटर
= 4070 वर्ग मीटर
Ans. 4070 वर्ग मीटर

Q.4 70 सेंटीमीटर आधार त्रिज्या और 40040 सेंटीमीटर के वक्रपृष्ठ क्षेत्र वाले लम्ब वृत्तीय शंकु का आयतन होगा?
A. 862400 सेंटीमीटर³
B. 863200 सेंटीमीटर³
C. 862200 सेंटीमीटर³
D. 865800 सेंटीमीटर³

हल:- प्रश्नानुसार,
शंकु का वक्रप्रष्ठ = πrl
= 40040
l = 182 सेंटीमीटर
h² = l² – t²
h² = (182)² – (70)²
h² = 28224
h = 168
शंकु का आयतन = ⅓ πr²h
= ⅓ × 22/7 × (70)² × 168
= 862400 सेंटीमीटर
Ans. 862400 सेंटीमीटर³

Q.5 14 सेंटीमीटर त्रिज्या और 20 सेंटीमीटर ऊँचाई के किसी वृत्ताकार बेलनाकार टुकड़े को ढालकर इतनी ही त्रिज्या वाले आधार का एक ठोस शंकु बनाया गया। शंकु की ऊँचाई क्या होगी?
A. 36 सेंटीमीटर
B. 40 सेंटीमीटर
C. 60 सेंटीमीटर
D. 68 सेंटीमीटर

हल:- माना ठोस शंकु की ऊँचाई = h सेंटीमीटर
⅓ × π × (14)² × h
= π × (14)² × 20
h = 60 सेंटीमीटर
Ans. 60 सेंटीमीटर

Q.6 एक 4 सेंटीमीटर व 8 सेंटीमीटर व्यास के खोखले गोले को गलाकर एक 8 सेंटीमीटर व्यास के आधार वाला शंकु बनाएं तो शंकु की ऊँचाई होगी?
A. 12 सेंटीमीटर
B. 18 सेंटीमीटर
C. 14 सेंटीमीटर
D. 15 सेंटीमीटर

हल:- प्रश्नानुसार,
माना शंकु की ऊँचाई = h सेंटीमीटर
⅓ π × 4(4)² × h
⁴⁄₃ π [(8/2)³ – (4/2)³]
h = 14 सेंटीमीटर
Ans. 14 सेंटीमीटर

जरूर पढ़िए : गणित के सूत्र

उम्मीद हैं आपको शंकु की जानकारी पसंद आयी होगी।

यदि आपको यह पोस्ट पसंद आयी हो तो दोस्तों के साथ जरूर शेयर करें।