इस पेज पर आप गणित के महवत्पूर्ण अध्याय परिमेय संख्या की जानकारी को पढ़ेंगे।
पिछले पेज पर हम अपरिमेय संख्या की जानकारी शेयर कर चुके है उसे जरूर पढ़े।
चलिए इस पेज पर परिमेय संख्या की परिभाषा, प्रकार और उदाहरण की जानकारी पढ़ते हैं।
परिमेय संख्या क्या है
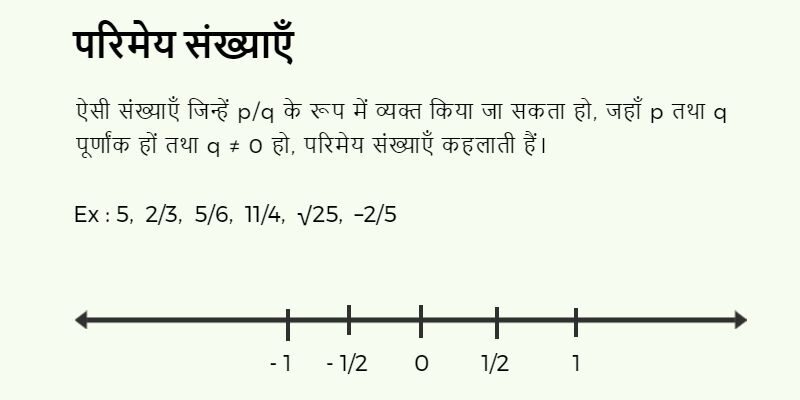
ऐसी संख्याएँ जिन्हें p/q के रूप में व्यक्त किया जा सकता हो, जहाँ p तथा q पूर्णांक हों तथा q ≠ 0 हो, परिमेय संख्याएँ कहलाती हैं।
(q या हर का मान जीरो नहीं होना चाहिए)
Ex :- 5, 2/3, 5/6, 11/4, √25, –2/5
परिमेय संख्या को अंग्रेजी में “Rational Number” कहते हैं।
अंश तथा हर
एक परिमेय संख्या जो कि p/q के रूप में होता है। p को अंश तथा q को हर कहते हैं।
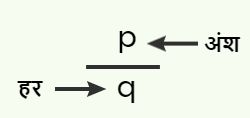
- परिमेय संख्या 5/7 में 5 अंश तथा 7 हर है।
- –6/7, जो कि एक परिमेय संख्या है, इसमें –6 अंश तथा 7 हर है।
- 12/–13 जो कि एक परिमेय संख्या है, इसमें 12 अंश तथा –13 हर है।
- 11/4 जो कि एक परिमेय संख्या है, इसमें 11 अंश तथा 4 हर है।
Note :-
- यदि दशमलव भिन्न वाली संख्याओं में दशमलव के बाद वाली संख्याओं की गिनती हो रही हो या दशमलव के बाद वाली संख्याओं की पुनरावर्ती हो रही हो। तो ऐसी संख्याएँ परिमेय संख्याए कहलाती हैं।
जैसे :- 1, 2, 3, 1/2, 2/5
धनात्मक एवं ऋणात्मक परिमेय संख्याएँ
परिमेय संख्या p/q के रूप की होती है, जहाँ p/q दोनों पूर्णांक होते है। q या हर हमेशा शून्य के बराबर नही होता है। परिमेय संख्याएँ धनात्मक और ऋणात्मक हो सकती हैं।
संख्याएँ धनात्मक परिमेय होगी यदि और केवल यदि (+p/+q) हो ऋणात्मक परिमेय होगा यदि और केव यदि -(p/q) हो।
| धनात्मक परिमेय | ऋणात्मक परिमेय |
|---|---|
| परिमेय संख्या जिनमें अंश तथा हर दोनों धनात्मक हों, धनात्मक परिमेय संख्या कहलाती हैं। | परिमेय संख्या जिनमें अंश या हर कोई एक ऋणात्मक हो ऋणात्मक परिमेय संख्या कहते हैं। |
| अंश और हर दोनों में बराबर चिन्ह हो। अर्थात (p/q) या (+p/+q) हो वह धनात्मक परिमेय संख्याएँ होगी। | यदि अंश और हर दोनों एक दूसरे के विपरीत चिन्ह के हो, अर्थात -(p/q) = (-p)/q = p/(-q), हो तो वह ऋणात्मक परिमेय संख्याएँ कहलाती हैं। |
| धनात्मक परिमेय संख्याएँ शून्य से बड़ी होती हैं। | ऋणात्मक परिमेय संख्याएँ शून्य से छोटी होती हैं। |
| धनात्मक परिमेय संख्या के उदाहरण :- 2/3, 4/5, 5/6, 6/7, 2.1 | धनात्मक परिमेय संख्या के उदाहरण :- 2/-3, 5/-7, -6/7, – 2.1 |
परिमेय संख्या से संबंधित प्रश्न और हल
Q.1 1/2 तथा 1/3 की तुलना कीजिए?
हल:- प्रश्नानानुसार,
1/2 तथा 1/3
इन दोनों परिमेय संख्याओं के हर 2 तथा 3 का लघुत्तम समापवर्तक होता है 3 × 2 =6
अत: 1/2 = (1 × 3)/(2 × 3) = 3/6
तथा, 1/3 = (1 × 2)/(3 × 2) = 2/6
अब चूँकि 3/6 तथा 2/6 के अंश में 6 बड़ा है अत:
3/6 > 2/6
या, 1/2 > 1/3
अर्थात 1/2 बड़ा है 1/3 से।
Q.2 -2/3 तथा 3/4 की तुलना कीजिए?
हल:- प्रश्नानानुसार,
ऋणात्मक संख्या धनात्मक संख्या से छोटी होती है।
दी गई परिमेय संख्याओं में -2/3 तथा 3/4 में -2/3 ऋणात्मक परिमेय संख्या हैं।
अतः -2/3 छोटा हैं 3/4 से
या -2/3 < 3/4
Q.3 परिमेय संख्या 3/5 तथा 6/7 की तुलना कीजिए?
हल:- प्रश्नानानुसार,
दी गयी परिमेय संख्या 3/5 तथा 6/7
बज्र गुणन करने पर
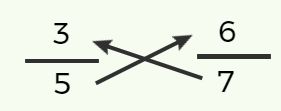
3 × 7 तथा 6 × 5
21 तथा 30
21 < 30
अत: 3/5 < 6/7
अर्थात, 3/5 छोटा है 6/7 से
Q.4 परिमेय संख्याओं 3 तथा 5 के बीच 3 परिमेय संख्या निकालें?
हल:- प्रश्नानानुसार,
दी गई परिमेय संख्याएँ हैं, 3 तथा 5
चरण 1. इन दी गई संख्याओं को p/q के रूप में लिखें
3 = 3/1 तथा 5 = 5/1
चरण 2. दी गई संख्याओं के बीच जितनी परिमेय संख्या निकालना है उसमें 1 जोड़ें।
चूँकि दी गई परिमेय संख्याओं के बीच 3 परिमेय संख्या निकालना है, अत: 3+1 = 4
चरण 3. दी गई परिमेय संख्याओं के अंश तथा हर को 4 से गुणा करें।
3/1 = (3 × 4)/(1 × 4) = 12/4
तथा 5/1 = (5 × 4)/(1 × 4) = 20/4
चरण 4. अब प्राप्त परिमेय संख्याओं के बीच की तीन परिमेय संख्यां को निकालें।
स्पष्टत: 12/4 तथा 20/4 के बीच परिमेय संख्याएँ हैं।
12/4 तथा 20/4
13/4, 14/4, 15/4, 16/4, 17/4, 18/4 तथा 19/4
जरूर पढ़िए : संख्या पद्धति
यदि आपको परिमेय संख्या का यह आर्टिकल पसंद आया हो तो अपने दोस्तों के साथ जरूर शेयर कीजिए।
यदि आप परिमेय संख्या से संबंधित अधिक जानकारी प्राप्त करना चाहते हैं तो कमेंट करें।