ग्राफ की परिभाषा, ग्राफ के प्रकार और उदाहरण

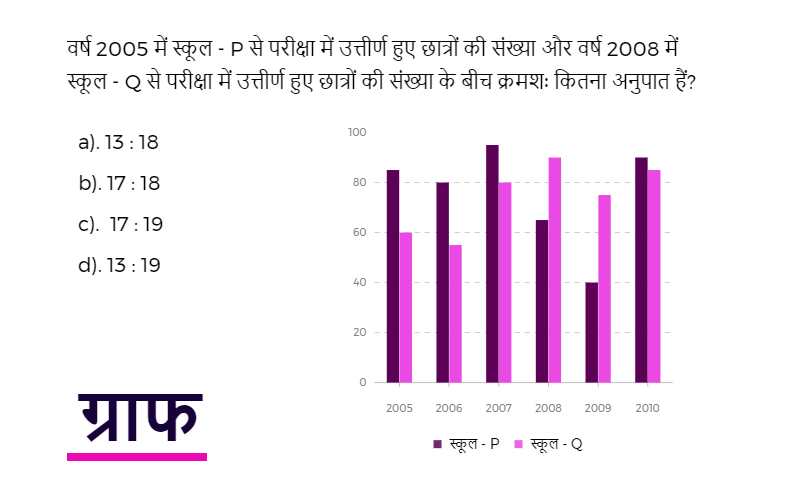
इस पेज पर आप गणित के महत्वपूर्ण अध्याय ग्राफ की जानकारी को पढ़ेंगे जो समस्त परीक्षाओं के लिए महत्वपूर्ण है।

पिछले पेज पर हमने गणित के महत्वपूर्ण अध्याय लाभ-हानि की जानकारी शेयर की है तो उस पोस्ट को जरूर पढ़े।

चलिए आज हम ग्राफ की परिभाषा, ग्राफ के प्रकार और उदाहरण को पढ़ते और समझते हैं।

ग्राफ क्या है

दो चर राशियो के बीच वर्गीकृत कागज पर एक दूसरे के प्रति सम्बन्ध दिखाने के लिए जिस सशक्त विधि का प्रयोग किया जाता हैं उसे ग्राफ कहते है।

ग्राफ के प्रकार

ग्राफ की उपयोगिता के आधार पर ग्राफ दो प्रकार का होता है।

1. सामान्य उपयोग के ग्राफ

सामान्य उपयोग के ग्राफ के सामान्य तरीके के कार्य में लिए जाते हैं। जिसका हमें आसानी से उपयोग होता हुआ दिखाई देता है।

जिस किसी क्षेत्र में ग्राफ की आवश्यकता होती है सामान्यत: इसी के अंतर्गत आने वाले ग्राम का उपयोग किया जाता है।

सामान्य उपयोग के ग्राफ के अंतर्गत चार प्रकार के ग्राफ को रखा गया है।

रेखा आलेख (Line Graph)
दंड आलेख (Bar Graph)
वृत्त आलेख (Pie Graph)
चित्रात्मक आलेख (Pictorial Graph)

यह चारों प्रकार के आलेख सामान्य उपयोग के अंतर्गत आते हैं।

नीचे आप सामान्य उपयोग के ग्राफ को विस्तार से पढ़िए और समझिए।

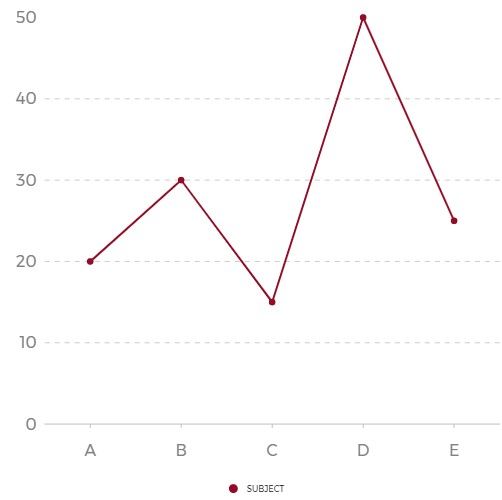
(a). रेखा आलेख (Line Graph)

रेखा ग्राफ सबसे अधिक उपयोग में आने वाला ग्राफ है। यह ग्राफ किसी भी क्षेत्र में उपयोग में किया जाने वाला सबसे आसान ग्राफ है। रेखा आलेख बनाना बहुत आसान है।

ग्राफ में एकत्र किए गए आंकड़ों को ग्राफ में X-अक्ष और Y-अक्ष के आधार पर पहले बिंदुवार अंकित करते हैं। इसके बाद इन बिंदुओं को मिलाते हैं। जिससे एक रेखा प्राप्त होती है इसलिए इसे रेखा आलेख या लाइन ग्राफ कहते हैं।

यदि हमें दो वर्गों के आंकड़ों में तुलना करना है तो दोनों आंकड़ों का अलग अलग लाइन एक ही ग्राफ में अंकित करना होगा जिससे दोनों में तुलना करने में बहुत आसानी होगी।

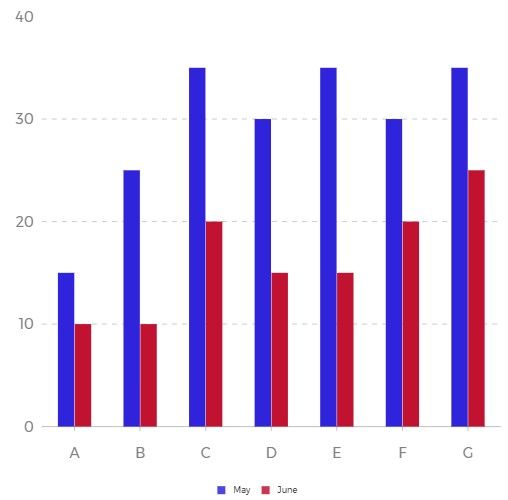
(b). दंड आलेख (Bar Graph)

दण्ड आलेख आंकड़ों को प्रदर्शित करने का एक आसान माध्यम है। इसमें दंड को X और Y अक्ष के सापेक्ष दर्शाया जाता है।

इसे बनाते समय इस बात का ध्यान रखना चाहिए कि प्रत्येक दंड आलेख की चौड़ाई समान हो तथा इनके बीच का अंतर भी समान हो। इसे ऊर्ध्वाधर तथा क्षैतिज दोनों तरह का बनाते हैं।

जब बार की संख्या इतनी अधिक हो कि इसे ऊर्ध्वाधर रूप में प्रदर्शित करना संभव ना हो तब हम क्षैतिज बार का प्रयोग करते हैं।

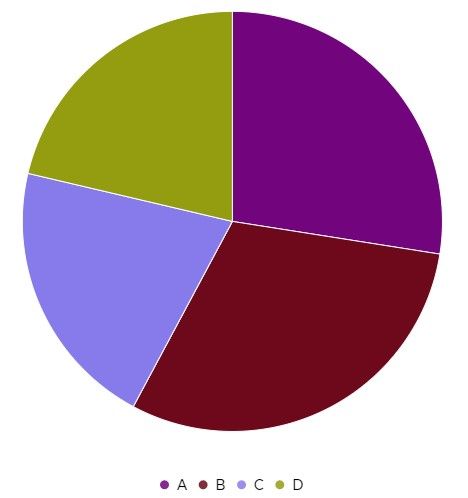
(c). वृत्त आलेख (Pie Graph)

व्रत आलेख को Circle Graph, Pie Chart भी कहते हैं।

इसका आकार वृत्तीय होता है। जैसा कि वृत्त के केंद्र बिंदु पर 360° का कोण होता है। इन्हें अलग-अलग विभिन्न भागों में एक-एक त्रिज्या खींचकर बांटा जा सकता है।

इसी प्रकार विभिन्न अवयव को या भागों को एक दूसरे से कितना संबंध है दर्शाने के लिए व्रत आलेख का उपयोग करते हैं।

(d). चित्रात्मक आलेख (Pictorial graph)

चित्रात्मक आलेख में जिस संदर्भ में ग्राफ बनता है उसके चित्रों को प्रदर्शित किया जाता है। जैसा कि नीचे ग्राफ में दर्शाया गया है।

2. विशेष उद्देश्य हेतु ग्राफ

किसी विशेष उद्देश्य की पूर्ति के लिए विशेष प्रकार के ग्राफ बनाने की आवश्यकता होती है।

इस प्रकार के ग्राफ में आसानी से हम अपनी जरूरतें पूरी कर सकते हैं। इस प्रकार के ग्राफ निम्न होते है।

क्षेत्र आलेख (Strata Graph)
फ्लोट आलेख (Float Graph)
बेल्ट आलेख (Belt Graph)
पिरामिड आलेख (Pyramid Graph)
मिश्रित आलेख (Compound Graph)
जी आलेख (Zee Graph)
रडार आलेख (Radar Graph)

अब हम इन आलेखों को कैसे उपयोग में लाना है इसके बारे में समझेंगे तथा यह आलेख क्या है यह भी जानेंगे

(a). क्षेत्र आलेख (Strata Graph)

क्षेत्र आलेख बनाने के लिए प्रत्येक Component के आंकड़ों को एकत्र किया जाता है।

आंकड़ों को अवरोही क्रम में जमा कर उसका संचयी तैयार किया जाता हैं। अब प्रत्येक अवयव के Cumulative को ग्राफ में अंकित करके लाइन ग्राफ तैयार करते हैं।

(b). फ्लोट आलेख (Float Graph)

यह विशेष उद्देश्य की पूर्ति के लिए बनाया जाने वाला एक ग्राफ है जिसमें दो अलग पहलुओं को तुलना करना आसान हो जाता है। इस ग्राफ का उपयोग शेयर बाजार में शेयर के उतार-चढ़ाव को देखने के लिए किया जाता है।

(c). बेल्ट आलेख (Belt Graph)

यह एक प्रकार का बार ग्राफ है। इसमें प्रत्येक बार अपने आप में पाई ग्राफ की तरह जानकारी देता है। यह ग्राफ क्षैतिज और ऊर्ध्वाधर दोनों तरीके से बनता है। यह ग्राफ प्रतिशत और मात्रा दोनों के आधार पर बनता है।

(d). पिरामिड आलेख (Pyramid Graph)

पिरामिड ग्राफ 3 या 3 से अधिक स्वतंत्र वेरिएबल जो एक दूसरे पर निर्भर नहीं करते उनका तुलनात्मक अध्ययन के लिए बनने वाला ग्राफ है।

(e). मिश्रित आलेख (Compound Graph)

कंपाउंड ग्राफ दो ग्राफ का मिश्रण रहता है। जैसे कि परेटो डायग्राम में बार ग्राफ और लाइन ग्राफ एक साथ होते हैं।

यह एक कंपाउंड ग्राफ है। इस ग्राफ का उपयोग परेटो डायग्राम बनाने के लिए किया जाता है।

(f). जी आलेख (Gee Graph)

इस प्रकार के ग्राफ में 3 तरह के आंकड़े लिए जाते हैं। इसमें मासिक आंकड़े, उनका Cumulative तथा पिछले 12 महीने का Cumulative लिए जाते हैं।

तथा इन्हें ग्राफ में अंकित करने पर Z आकार का वक्र प्राप्त होता है। इस ग्राफ में जिस महीने के आंकड़ों को समझना रहता है उसे आसानी से पता कर लेते हैं।

(g). रडार आलेख (Radar Graph)

रडार ग्राफ को हम उदाहरण द्वारा समझेंगे।

मान लीजिए आपके कॉलेज में अलग-अलग विषयों पर एक सेमिनार का आयोजन होता है। आयोजन शुरू होने के पहले आप से टेस्ट लिया जाता है तब प्रत्येक विषय में विद्यार्थियों को कितना प्रतिशत अंक प्राप्त हुए उसे ग्राफ में अंकित कर लेते हैं।

सेमिनार समाप्त होने के बाद फिर से आप से टेस्ट लिया जाता है । अब प्राप्त अंकों को उसी ग्राफ में अंकित करते हैं।

इससे पता चलता है कि आपको कौन से विषय में सुधार करने की आवश्यकता है।

ग्राफ को उदाहरण द्वारा समझते हैं।

उदाहरण : निम्लिखित ग्राफ में किसी कम्पनी द्वारा कुछ वर्षों में किए गए वस्त्रों का निर्माण (हजारों में) दर्शाया गया हैं। आपको बताना हैं कि 1990 में 1989 की तुलना में निर्माण में कितने प्रतिशत की कमी हुई हैं?

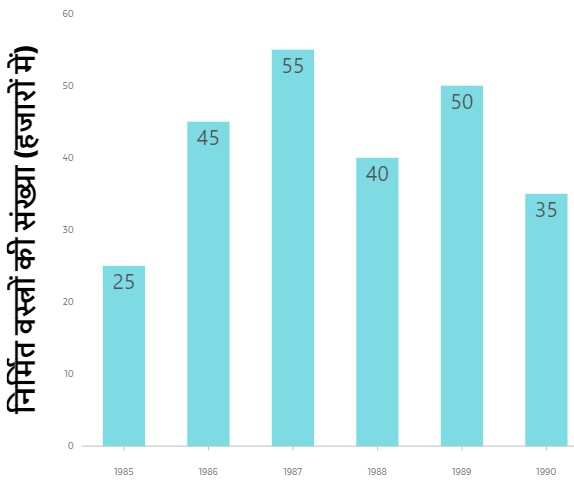
हल:- 1990 में 1989 की तुलना में निर्माण में प्रतिशत कमी
= (50 – 35)/50 × 100
= 15/50 × 100
= 30%

ग्राफ से सम्बन्धित प्रश्न-उत्तर

प्रश्न 1. निम्लिखित चार्ट में 5 कम्पनियों A, B, C, D, E की माँग और उनके उत्पादन को दर्शाया गया हैं।

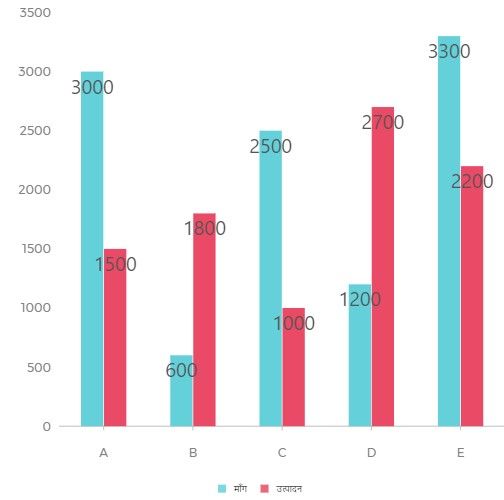
ग्राफ को ध्यानपूर्वक अध्ययन कर नीचे दिए गए प्रश्नों के उत्तर दें?

(A). यदि कम्पनी C की मांग का x% कम्पनी B की माँग के बराबर हैं, तो x किसके बराबर हैं?
(a). 4
(b). 24
(c). 20
(d). 60

C की माँग × x% = B की माँग
2500 × x/100 = 600
x = (600 × 100)/2500
x = 24

(B). यदि A किसी कम्पनी के अधिशेष उत्पादन को खरीदकर अपनी मांग को पूरा करना चाहती हैं, तो सबसे उपयुक्त कंपनी कौन सी हैं?
(a). B
(b). C
(c). D
(d). E

A → 3000 – 1500 = 1500
D → 2700 – 1200 = 1500
अभीष्ट उत्तर = D

(C). यदि D कम्पनी का उत्पादन A कम्पनी के उत्पादन का h गुना हैं, तो h किसके बराबर हैं?
(a). 1.8
(b). 1.5
(c). 2.5
(d). 1.2

D कम्पनी का उत्पादन = A कम्पनी के उत्पादन × h
2700 = 1500 × h
h = 2700/1500
h = 1.8

(D). पाँचों कम्पनियों को मिलाकर उनकी औसत माँग और उनके औसत उत्पादन में अंतर हैं?
(a). 620
(b). 400
(c). 280
(d). 130

औसत माँग = (3000 + 600 + 2500 + 1200 + 3300)/5
= 10600/5
= 2120
औसत उत्पादन = (1500 + 1800 + 1000 + 2700 + 2200)/5
= 9200/5
= 1840
अभीष्ट अंतर = 2120 – 1840
= 280

(E). उत्पादन से अधिक माँग वाली कंपनियों का और माँग से अधिक उत्पादन वाली कंपनियों का अनुपात हैं?
(a). 2 : 3
(b). 4 : 1
(c). 2 : 2
(d). 3 : 2

A, C, E → उत्पादन से अधिक माँग
B, D → माँग से अधिक उत्पादन
अभीष्ट उत्तर = 3 : 2

प्रश्न 2. निम्लिखित दण्ड आलेख 10 वीं कक्षा के छात्रों का 4 वर्ष की परीक्षा परिणाम दर्शाता हैं। आरेख का अध्ययन कीजिए और निम्लिखित प्रश्नों का उत्तर दीजिए।

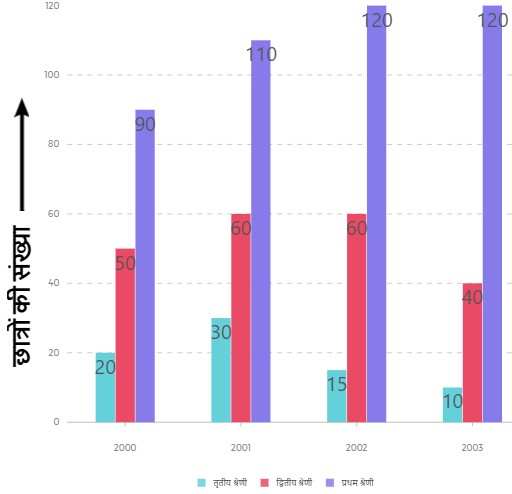
(A). वर्ष 2002 में 10 वीं कक्षा की परीक्षा में शामिल छात्रों की संख्या हैं?
(a). 180
(b). 195
(c). 200
(d). 120

वर्ष 2002 में छात्रों की अभीष्ट संख्या = 15 + 60 + 120
= 195

(B). वर्ष 2002 की तुलना में वर्ष 2003 में प्रथम श्रेणी में प्रतिशत वृद्धि बताइए?
(a). 12%
(b). 0%
(c). 10%
(d). 9%

अभीष्ट प्रतिशत वृद्धि = (120 – 120) × 100
= 0%

(C). किस वर्ष में 10 वीं कक्षा की परीक्षा में छात्र अधिकतम संख्या में शामिल हुए?
(a). 2001
(b). 2002
(c). 2003
(d). 2000

छात्रों की संख्या :
वर्ष 2000 = 20 + 50 + 90 = 160
वर्ष 2001 = 30 + 60 + 110 = 200
वर्ष 2002 = 195
वर्ष 2003 = 170
अभीष्ट वर्ष = 2001

(D). वर्ष 2000 में शामिल द्वितीय श्रेणी प्राप्त करने वाले और परीक्षा में शामिल कुल छात्रों का अनुपात बताइए?
(a). 3 : 16
(b). 4 : 17
(c). 5 : 16
(d). 11 : 16

अभीष्ट अनुपात = 50 : 160
= 5 : 16

प्रश्न 3. निम्न लेखाचित में, एक फैक्ट्री में 50 श्रमिकों की दैनिक मजदूरी को दर्शाया गया हैं। इसका अध्ययन कर निम्न प्रश्नों के उत्तर दीजिए।

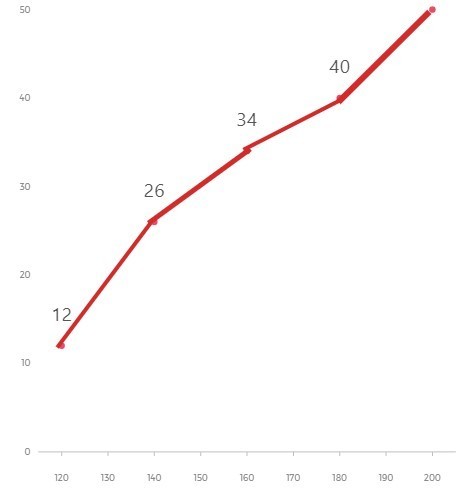
(A). कितने प्रतिशत श्रमिक की आय 150 रुपए से 180 रुपए के बीच हैं?
(a). 6%
(b). 16%
(c). 12%
(d). 20%

मजदूरी	संचयी बारम्बारता	श्रमिकों की संख्या
120	12	12
140	26	26 – 12 = 14
160	34	34 – 26 = 8
180	40	40 – 34 = 6
200	50	50 – 40 = 10

अभीष्ट प्रतिशत = 8/50 × 100
= 16%

(B). फैक्ट्री में मजदूरी की माध्यिका कितनी हैं?
(a). 140
(b). 138
(c). 150
(d). 160

माध्यिका = (न्यूतम मान + अधिकतम मान)/2
= (120 + 200)/2
= 320/2
= 160 रुपए

प्रश्न 4. निम्न दण्ड आरेख नगर के किसी विशिष्ट इलाके में छात्रों द्वारा स्कूल तक जाने के लिए प्रयोग में की जाने वाली विभिन्न विधियों को निरूपित करता हैं।

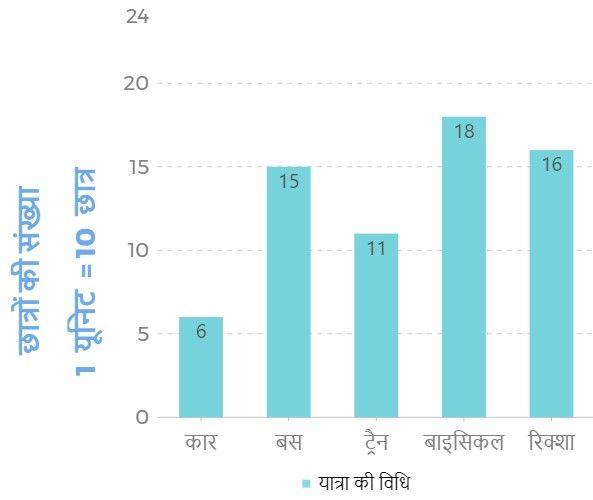
(A). उस इलाके में कितने छात्र आते हैं?
(a). 500
(b). 600
(c). 560
(d). 660

छात्रों की कुल संख्या
= (6 + 15 + 11 + 18 + 16) × 10
= 66 × 10
= 660 छात्र

(B). कितने छात्र मिलकर बाइसिकल और रिक्शा का प्रयोग करते हैं?
(a). 240
(b). 340
(c). 140
(d). 440

बाइसिकल एवं रिक्शा प्रयोक्ता छात्र
= (18 + 16) × 10
= 340 छात्र

(C). उस इलाके में बस का प्रयोग करने वाले छात्रों का प्रतिशत हैं?
(a). 110/7
(b). 250/11
(c). 306/17
(d). 240/17

बस का प्रयोग करने वाले छात्र = 150
अभीष्ट प्रतिशत = 150/660 × 100
= 250/11

(D). परिवहन के अपने साधन के रूप में कार का और रिक्शा का प्रयोग करने वाले छात्रों का अनुपात हैं?
(a). 7 : 2
(b). 8 : 3
(c). 2 : 7
(d). 3 : 8

अभीष्ट अनुपात = 6 : 16
= 3 : 8

प्रश्न 5. निम्न दण्ड आरेख वर्ष 2000 से 2006 तक आलू का उत्पादन (क्विंटल में) दर्शाया हैं। आरेख का अध्ययन करें और प्रश्नों का उत्तर दें?

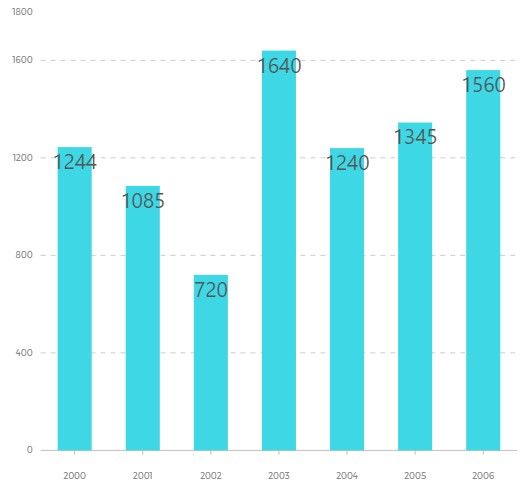
(A). इस अवधि के दौरान औसत उत्पादन को देख कर, उन वर्षों की संख्या क्या हैं जिनमें उत्पादन औसत से अधिक हुआ हैं?
(a). 1
(b). 2
(c). 3
(d). 4

औसत उत्पादन = (1244 + 1085 + 720 + 1640 + 1240 + 1345 + 1560) × 1/7
= 8834/7
= 1262 क्विंटल
औसत उत्पादन से अधिक का वर्ष
= 2003, 2005, 2006
= 3

(B). इस अवधि के दौरान उत्पादन में अधिकतम हास की दर हैं?
(a). 24.4%
(b). 28.22%
(c). 33.64%
(d). 35.32%

हास का प्रतिशत :
वर्ष 2004 = 400/1640 × 100
= 24.4%
वर्ष 2002 = (1085 – 720) × 100/1085
= 365/1085 × 100
= 33.64%
वर्ष 2001 = (1244 – 1085)/1244 × 100
= 159/1244 × 100
= 12.78%
अधिकतम हास 33.64% था।

प्रश्न6. निम्लिखित ग्राफ एवं सारिणी का ध्यान से अध्ययन कर नीचे दिए गए प्रश्नों के उत्तर दीजिए?

अलग-अलग दो दिनों में छह वाहनों द्वारा यात्रा करने में लगा समय (घण्टों में)

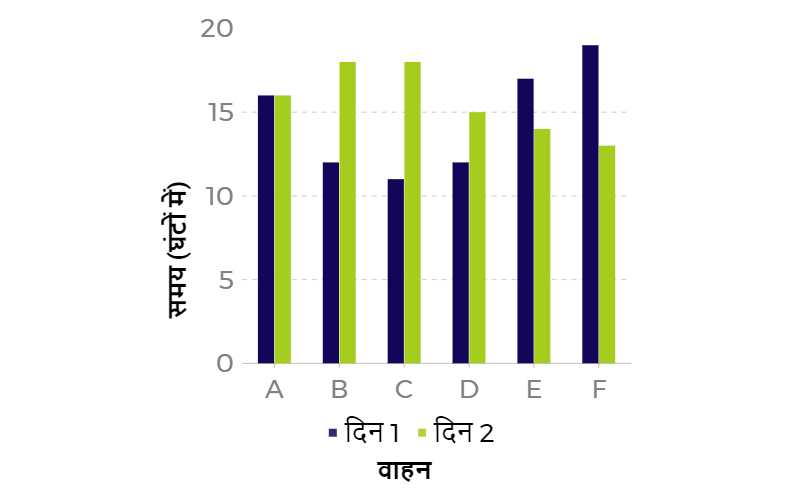
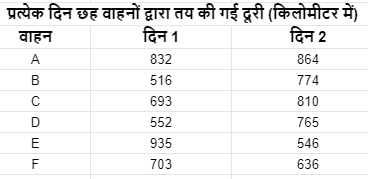
(A). निम्लिखित में से कौन-सा वाहन दोनों दिन समान गति से चला था?
(a). वाहन A
(b). वाहन C
(c). वाहन F
(d). वाहन B

वाहन B की गति
पहला दिन = 516/12
= 43 किमी/घण्टा
दूसरा दिन = 774/18
= 43 किमी/घण्टा

(B). पहले दिन वाहन A की गति और उसी दिन वाहन C की गति के बीच क्या अंतर था?
(a). 7 किमी/घण्टा
(b). 12 किमी/घण्टा
(c). 11 किमी/घण्टा
(d). 8 किमी/घण्टा

= (693/11 – 832/16) किमी/घण्टा
= (63 – 52) किमी/घण्टा
= 11 किमी/घण्टा

(C). मीटर प्रति सेकण्ड में दूसरे दिन वाहन C की गति क्या थी?
(a). 15.3
(b). 12.8
(c). 11.5
(d). 13.8

वाहन C की गति = (810/18) किमी/घण्टा
= 810/18 × 5/18 मी/से.
= 12.5 मी/से.

(D). वाहन F द्वारा दूसरे दिन तय की गई दूरी उसके द्वारा पहले दिन तय की गई दूरी का लगभग कितना प्रतिशत हैं?
(a). 80%
(b). 65%
(c). 85%
(d). 90%

वाहन F द्वारा दूरी % = 636/703 × 100
= 640/700 × 100
= 91.42
= 90%

(E). दूसरे दिन वाहन D और वाहन E की गति के बीच क्रमशः अनुपात क्या था?
(a). 15 : 13
(b). 17 : 13
(c). 13 : 11
(d). 17 : 14

अभीष्ट अनुपात = D : E
= 765/15 = 546/14
= 51 : 39
= 17 : 13

जरूर पढ़े:
क्षेत्रमिति	साधारण ब्याज	अनुपात और समानुपात
त्रिकोणमिति	चक्रवृद्धि ब्याज	ऊंचाई और दूरी

उम्मीद हैं आपको ग्राफ की जानकारी पसंद आयी होगी।

ग्राफ से संबंधित किसी भी प्रश्न के लिए कमेंट करे।

यदि ग्राफ की जानकारी पसंद आयी है तो इसे अपने दोस्तों साथ शेयर करना ना भूले।